按要求画出图形并填空
(1)点C在直线AB上,点P在直线AB外;
(2)过点P画PD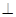 AB,垂足为点D;
AB,垂足为点D;
(3)P、C两点间的距离是线段 的长度;
(4)点P到直线AB的距离是线段 的长度.
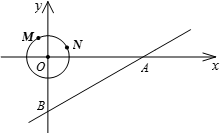
如图,以直角坐标系的原点O作⊙O,点M、N是⊙O上的两点,M(-1,2),N(2,1)试在x轴上找出点P使PM+PN最小,求出P的坐标;
若在坐标系中另有一直线AB,A(10,0),点B在y轴上,∠BAO=30°,⊙O以0. 2个单位/秒的速度沿x轴正方向运动,问圆在运动过程中与该直线相交的时间有多长?
某批发商以每件50元的价格购进800件衬衣,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计可售出200件,批发商为增加销售,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的衬衣一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.填写下表
| 时间 |
第一个月 |
第二个月 |
清仓时 |
| 单价(元) |
80 |
40 |
|
| 销量(件) |
200 |
如果批发商销售这批衬衣后获利9000元,求第二个月的单价是多少?
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.求证:直线PB与⊙O相切;
PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4,求CE的长.

上海世博会门票价格如下表所示:
| 指定日普通票(张) |
200元 |
| 平日优惠票(张) |
100元 |
某旅行社准备了1300元,全部用来购买指定日普通票和平日优惠票,且每种至少买一张.有多少种购票方案?列举所有可能结果;
如果从上述方案中任意选择一种方案购票,求恰好选到11张门票的概率.
已知一元二次方程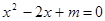 .
.若方程有两个实数根,求m的范围;
若方程的两实根为x1,x2,且
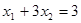 ,求m的值.
,求m的值.