(本题满分14分) 设函数f (x)=ln x+ 在(0,
在(0, ) 内有极值.
) 内有极值.
(Ⅰ) 求实数a的取值范围;
(Ⅱ) 若x1∈(0,1),x2∈(1,+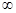 ).求证:f (x2)-f (x1)>e+2-
).求证:f (x2)-f (x1)>e+2- .
.
注:e是自然对数的底数.
(本小题满分12分)将圆 按向量
按向量 平移得到
平移得到 ,直线
,直线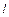 与
与 相交于
相交于 、
、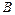 两点,若在
两点,若在 上存在点
上存在点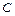 ,使
,使 求直线
求直线 的方程.
的方程.
(本小题满分12分)最近,李师傅一家三口就如何将手中的10万块钱投资理财,提出了三种方案:
第一种方案:李师傅的儿子认为:根据股市收益大的特点,应该将10万块钱全部用来买股票. 据分析预测:投资股市一年可能获利40%,也可能亏损20%.(只有这两种可能),且获利的概率为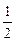 .
.
第二种方案:李师傅认为:现在股市风险大,基金风险较小,应将10万块钱全部用来买基金. 据分析预测:投资基金一年后可能获利20%,可能损失10%,也可能不赔不赚,且这三种情况发生的概率分别为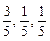 .
.
第三种方案:李师傅妻子认为:投入股市、基金均有风险,应该将10万块钱全部存入银行一年,现在存款年利率为4%,存款利息税率为5%.
针对以上三种投资方案,请你为李师傅家选择一种合理的理财方法,并说明理由.
(本小题满分12分)
设锐角三角形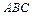 的内角
的内角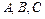 的对边分别为
的对边分别为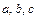 ,且
,且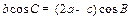 .
.
(Ⅰ)求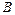 的大小;
的大小;
(Ⅱ)求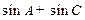 的取值范围.
的取值范围.
已知,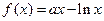 ,
,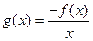 ,
,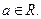
⑴当 时, 讨论
时, 讨论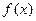 的单调性、极值;
的单调性、极值;
⑵当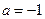 时,求证:
时,求证: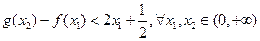 成立;
成立;
⑶是否存在实数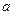 ,使
,使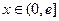 时,
时,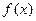 的最小值是3,若存在,求出
的最小值是3,若存在,求出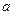 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知椭圆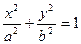 (a>b>0)
(a>b>0)
(1)当椭圆的离心率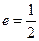 ,一条准线方程为x=4 时,求椭圆方程;
,一条准线方程为x=4 时,求椭圆方程;
(2)设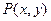 是椭圆上一点,在(1)的条件下,求
是椭圆上一点,在(1)的条件下,求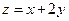 的最大值及相应的P点坐标。
的最大值及相应的P点坐标。
(3)过B(0,-b)作椭圆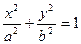 (a>b>0)的弦,若弦长的最大值不是2b,求椭圆离心率的取值范围。
(a>b>0)的弦,若弦长的最大值不是2b,求椭圆离心率的取值范围。