已知,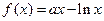 ,
,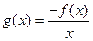 ,
,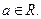
⑴当 时, 讨论
时, 讨论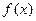 的单调性、极值;
的单调性、极值;
⑵当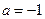 时,求证:
时,求证: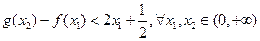 成立;
成立;
⑶是否存在实数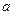 ,使
,使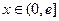 时,
时,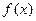 的最小值是3,若存在,求出
的最小值是3,若存在,求出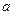 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知等差数列{an}满足a2=2,a5=8.
(1)求{an}的通项公式;
(2)各项均为正数的等比数列{bn}中,b1=1,b2+b3=a4,求{bn}的前n项和Tn.
解关于x的不等式 ≤
≤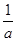 (其中a>0且a≠1).
(其中a>0且a≠1).
在数列{an}中,a1=1,an+1=2an+2n.
(1)设bn=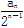 .证明:数列{bn}是等差数列;
.证明:数列{bn}是等差数列;
(2)求数列{an}的前n项和Sn.
在△ABC中,a、b、c分别是角A、B、C的对边,且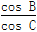 =-
=- .
.
(1)求角B的大小;
(2)若b= ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
等比数列{an}的各项均为正数,且2a1+3a2=1,a =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列 的前n项和.
的前n项和.