某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境:
如图2,将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M处,连接BF与EG交于点P.
所得结论:
当点F与AD的中点重合时:(如图1)甲、乙、丙三位同学各得到如下一个正确结论(或结果):
甲:△AEF的边AE= cm,EF= cm;
乙:△FDM的周长为16 cm;
丙:EG=BF.
你的任务:填充甲同学所得结果中的数据;
写出在乙同学所得结果的求解过程;
当点F在AD边上除点A、D外的任何一处(如图2)时:
① 试问乙同学的结果是否发生变化?请证明你的结论;
② 丙同学的结论还成立吗?若不成立,请说明理由,若你认为成立,先证明EG=BF,再求出S(S为四边形AEGD的面积)与x(AF=x)的函数关系式,并问当x为何值时,S最大?最大值是多少?
某学校准备购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
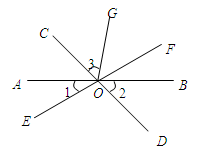
如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.
某学校对学生的课外阅读时间进行抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,并绘制成如下的统计图表(图中信息不完整).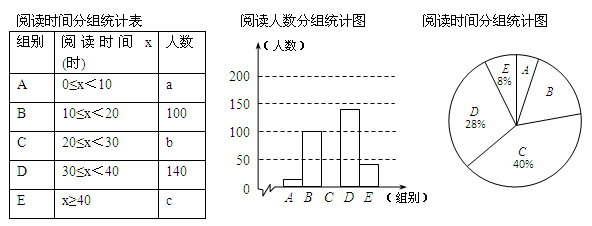
请结合以上信息解答下列问题
(1)求a、b、c的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在20小时以下(不含20小时)的学生所占比例.
某超市开业十周年举行了店庆活动,对A、B两种商品实行打折出售.打折前,购买5件A商品和1件B商品需用84元;购买6件A商品和3件B商品需用108元.而店庆期间,购买3件A商品和8件B商品仅需72元,求店庆期间超市的折扣是多少?
如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°.求∠3的度数.