在图1、图2中,线段AC=CE,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M.
如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,容易证明FM = MH,FM⊥HM;现将图1中的CE绕点C顺时针旋转一个锐角,得到图2,判断△FMH的形状,并证明你的结论.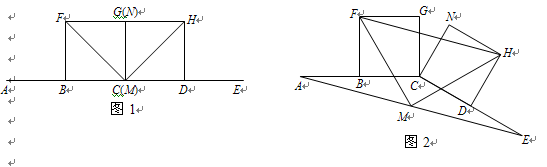
某位市民想为贫困山区的孩子们献一份爱心,准备购买一批书包捐赠给他们.经调查有这样的一种书包,原售价为每只150元,现A、B两家商店优惠出售,A商店一律8折出售;B商店规定:购买少于n只的书包,仍以原价出售,超过n只,其中n只书包的部分仍以原价出售,超地n只的部分,打a折出售.在A、B两商店购买x只书包所需的金额分别为y1(元)和y2(元),y1,y2与x的函数的图像如图所示.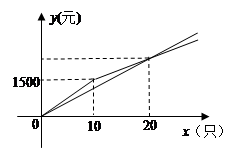
根据图象,可知a=__ ▲___,n=___ ▲___;
求y1,y2关于x的函数解析式;
由于颜色等原因,现该市民在A、B两商店共购买50只这种书包,共付款6240元,问他在A、B两家商店各购买书包多少只?
如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.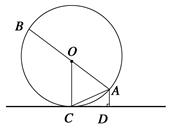
若∠AOC=48°,求∠ACD的度数;
若AB=8,AD=2,求AC的长
列方程或方程组解应用题:
“五一”节日期间,某超市进行积分兑换活动,具体兑换方法见右表. 爸爸拿出自己的积分卡,对小华说:“这里积有8200 分,你去给咱家兑换礼品吧”.小华兑换了两种礼品,共10件,还剩下了200分,请问她兑换了哪两种礼品,各多少件?
已知:如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.
求∠PCQ的度数
求证:∠APB=∠QPC.
某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.
请根据途中提供的信息,解答下列问题:
参加调查的人数共有▲人;在扇形图中,表示“其它球类”的扇形的圆心角为▲度;
将条形图补充完整;
若该校有2000名学生,则估计喜欢“篮球”的学生共有多少人?