小明在复习数学知识时，针对“利用函数求一元二次方程的解”整理了以下几种方法，请你将有关内容补充完整：
例题：求一元二次方程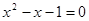
的两个解。（1）解法一：利用二次函数图象与两坐标轴的交点求解。
如图，把方程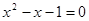的解看成是二次函数
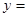__________的图象与
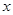轴交点的横坐标，即
，
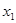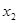就是方程的解。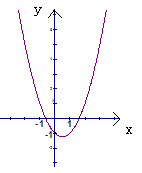
（2）解法二：利用两个函数图象的交点求解。
①把方程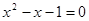的解看成是二次函数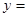_________的图象与一个一次函数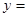_________的图象交点的横坐标。
②画出这两个函数的图象，用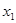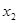，在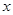轴上标出方程的解。
在“母亲节”期间，某校部分团员参加社会公益活动，准备购进一批许愿瓶进行
销售，并将所得利润捐给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量y(个)于销售单价x(元
/个)之间的对应关系如图所示．
(1)试判断y与x之间的函数关系，并求出函数关系式；
(2)若许愿瓶的进价为6元/个，按照上述市场调查销售规律，求利润w(元)与销售单价x(元/个)之间的
函数关系式；
(3)若许愿瓶的进货成本不超过900元，要想获得最大利润，试求此时这种许愿瓶的销售单价，并求出
最大利润．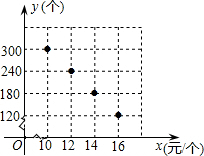
如图，四边形ABCD的对角线AC、BD交于点O，BE⊥AC于E，DF⊥AC于
F，点O既是AC的中点，又是EF的中点．
(1)求证：△BOE≌△DOF；
(2)若OA＝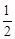
BD，则四边形ABCD是什么特殊四边形？请说明理由．
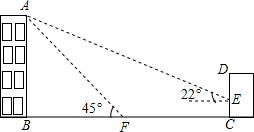
如图，某校教学楼AB的后面有一建筑物CD，当光线与地面的夹角是22º时，
教学楼在建筑物的墙上留下高2m的影子CE；而当光线与地面的夹角是45º时，教学楼顶A在地面上的影
子F与墙角C有13m的距离(B、F、C在一条直线上)．
(1)求教学楼AB的高度；
(2)学校要在A、E之间挂一些彩旗，请你求出A、E之间的距离(结果保留整数)．
(参考数据：sin22º≈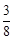
，cos22º≈
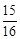，tan22º≈
)
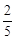小丽乘坐汽车从青岛到黄岛奶奶家，她去时经过环湾高速公路，全程约84km，
返回时经过跨海大桥，全程约45km．小丽所乘汽车去时的平均速度是返回时的1.2倍，所用时间却比返回
时多20min．求小丽所乘汽车返回时的平均速度．
某商场为了吸引顾客，举行抽奖活动，并规定：顾客每购买100元的商品，就
可以随机抽取一张奖券，抽得奖券“紫气东来”、“化开富贵”、“吉星高照”，就可以分别获得100元、50元、
20元的购物券，抽得“谢谢惠顾”不赠购物券；如果顾客不愿意抽奖，可以直接获得购物券10元，小明购
买了100元的商品，他看到商场公布的前10000张奖券的抽奖结果如下：
| 奖券种类 |
紫气东来 |
化开富贵 |
吉星高照 |
谢谢惠顾 |
| 出现张数(张) |
500 |
1000 |
2000 |
6500 |
(1)求“紫气东来”奖券出现的频率；
(2)请你帮助小明判断，抽奖和直接获得购物券，哪种方式更合算？说明理由．