将直线 向左平移2个单位后得到直线l,若直线l与反比例函数
向左平移2个单位后得到直线l,若直线l与反比例函数 的图象的交点为(2,-m).
的图象的交点为(2,-m).求直线l的解析式及直线l与两坐标轴的交点;
求反比例函数的解析式.
如图,求四边形ABCD的面积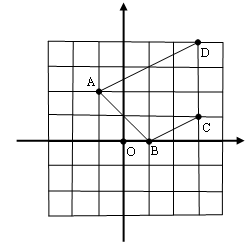
用一条长为18cm的细绳围成一个等腰三角形.
(1) 如果腰长是底边的2倍,那么各边的长是少?
(2)能围成有一边的长为4cm的等腰三角形吗?为什么?
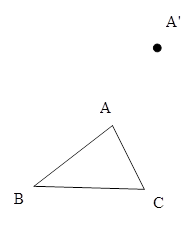
如图,平移三角形ABC,使点A移动到A′,画出平移后的三角形A′B′C′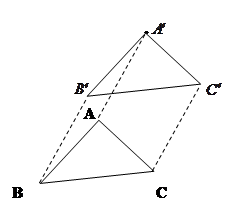
甲乙两车间生产一种产品,原计划两车间共生产300件产品,实际甲车
间比原计划多生产10%,乙车间比原计划多生产20%,结果共生产了340
件产品,问原计划甲、乙两车间各生产了多少件产品?
已知:∠B=∠2, ∠1=30°,求∠D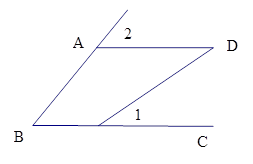
完成填空
解:∵∠2=∠B(已知)
∴AD//BC ( )
∴∠D=∠1 ( )
又∵∠1=30°
∴∠D=30° (等量代换)