(本题满分12分)如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB。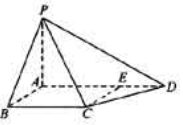
（1） 求证：CE⊥平面PAD；
（11）若PA=AB=1，AD=3，CD=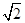
，∠CDA=45°，求四棱锥P-ABCD的体积
（本小题满分12分） 设
为数列
的前
项和，且对任意
时，点
都在函数
的图象上。
（1）求数列的通项公式；
（2）设
，求数列
的前项和
的最大值。
（本小题满分12分） 某校校庆，各界校友纷至沓来，某班共来了
位校友（
且
），其中女校友
位，组委会对这位校友登记制作了一份校友名单，现随机从中选出
位校友代表，若选出的位校友代表是一男一女，则称为“友情搭档”。
（1）若随机选出的位校友代表为“友情搭档”的概率不小于
，求的最大值；
（2）当
时，设选出的位校友代表中女校友人数为
，求的分布列和均值。
（本小题满分12分）在
中，角
的对边分别是
，若
。
（1）求角
的大小；
（2）若
，的面积为
，求
的值。
（本小题满分14分）已知函数
，
.
（1）求函数
的单调递增区间；
（2）若函数
有两个零点
，且
，求实数
的取值范围并证明
随的增大而减小.
（本小题满分13分）已知函数
（
，
）图象的相邻两对称轴间的距离为
，若将函数
的图象向左平移
个单位后图象关于
轴对称.
（1）求使
成立的
的取值范围；
（2）设
，其中
是
的导函数，若
，且
，求
的值.