某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线 ,在抛物线上任意画一个点
,在抛物线上任意画一个点 ,度量点
,度量点 的坐标
的坐标 ,如图.
,如图.
(Ⅰ)拖动点 ,发现当
,发现当 时,
时, ,试求抛物线
,试求抛物线 的方程;
的方程;
(Ⅱ)设抛物线 的顶点为
的顶点为 ,焦点为
,焦点为 ,构造直线
,构造直线 交抛物线
交抛物线 于不同两点
于不同两点 、
、 ,构造直线
,构造直线 、
、 分别交准线于
分别交准线于 、
、 两点,构造直线
两点,构造直线 、
、 .经观察得:沿着抛物线
.经观察得:沿着抛物线 ,无论怎样拖动点
,无论怎样拖动点 ,恒有
,恒有
 .请你证明这一结论.
.请你证明这一结论.
(Ⅲ)为进一步研究该抛物线 的性质,某同学进行了下面的尝试:在(Ⅱ)中,把“焦点
的性质,某同学进行了下面的尝试:在(Ⅱ)中,把“焦点 ”改变为其它“定点
”改变为其它“定点
 ”,其余条件不变,发现“
”,其余条件不变,发现“ 与
与 不再平行”.是否可以适当更改(Ⅱ)中的其它条件,使得仍有“
不再平行”.是否可以适当更改(Ⅱ)中的其它条件,使得仍有“
 ”成立?如果可以,请写出相应的正确命题;否则,说明理由.
”成立?如果可以,请写出相应的正确命题;否则,说明理由.
如图,在以点 为圆心, 为直径的半圆 中, , 是半圆弧上一点, ,曲线 是满足 为定值的动点 的轨迹,且曲线 过点 .
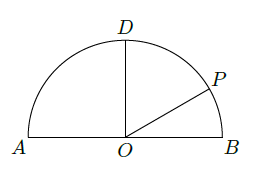
(Ⅰ)建立适当的平面直角坐标系,求曲线
的方程;
(Ⅱ)设过点
的直线
与曲线
相交于不同的两点
.若
的面积不小于
,求直线
斜率的取值范围.
如图,在三棱柱 中,平面 侧面
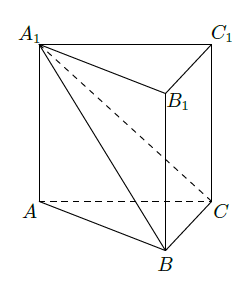
求证
(若直线 与平面 所成的角为 ,二面角 的大小为 ,试判断 与 的大小关系,并予以证明。
袋中有20个大小相同的球,其中记上0号的有10个,记上
号的有
个(
=1,2,3,4)。现从袋中任取一球.
表示所取球的标号.
(Ⅰ)求
的分布列,期望和方差;
(Ⅱ)若
,试求
的值。
已知函数f(t)= , , .
(Ⅰ)将函数
化简成
的形式;
(Ⅱ)求函数
的值域。
已知以
为首项的数列
满足:
(1)当
,
,
时,求数列
的通项公式;
(2)当
,
,
时,试用
表示数列
的前
项的和
;
(3)当
(
是正整数),
,
时,求证:数列
,
,
,
成等比数列当且仅当
.