由数字1、2、3、4、5、6组成无重复数字的数中,求:
(1)六位偶数的个数;
(2)求三个偶数互不相邻的六位数的个数;
(3)求恰有两个偶数相邻的六位数的个数;
(4)奇数字从左到右,从小到大依次排列的六位数的个数.
设函数 对任意实数x 、y都有
对任意实数x 、y都有 ,
,
(1)求 的值;
的值;
(2)若 ,求
,求 、
、 、
、 的值;
的值;
(3)在(2)的条件下,猜想
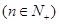 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
设数列 的前
的前 项和为
项和为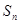 ,且
,且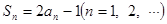 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,求数列
,求数列 的通项公式.
的通项公式.
复数 =
=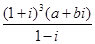 且
且 ,
, 对应的点在第一象限,若复数0,z,
对应的点在第一象限,若复数0,z, 对应的点是正三角形的三个顶点,求实数
对应的点是正三角形的三个顶点,求实数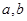 的值.
的值.
已知函数 (
( ).
).
(1)若函数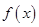 在
在 处取得极值,求
处取得极值,求 的值;
的值;
(2)在(1)的条件下,求证: ;
;
(3)当 时,
时,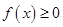 恒成立,求
恒成立,求 的取值范围.
的取值范围.