如图，在平面直角坐标系中，点O为坐标原点，以点A（0，-3）为圆心，5为半径作圆A，交x轴于B、C两点，交y轴于点D、E两点．（1）如果一个二次函数图象经过B、C、D三点，求这个二次函数的解析式；
（2）设点P的坐标为（m,0）(m>5),
过点P作
x轴交（1）中的抛物线于点Q，当以
为顶点的三角形与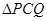
相似时，求点P的坐标．
某汽车专卖店销售A，B两种型号的新能源汽车，上周售出1辆A型车和3辆B型车，销售额为96万元，本周已售出2辆A型车和1辆B型车，销售额为62万元。
（1）求每辆A型车和B型车的售价各多少万元。
（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元，则有哪几种购车方案？
．甲、乙两人准备整理一批新到的图书，甲单独整理需要40分钟完工；若甲、乙共同整理20分钟后，乙需再单独整理30分钟才能完工．问乙单独整理这批图书需要多少分钟完工？
先化简：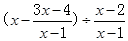
，再任选一个你喜欢的数
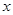代入求值．
解方程（组）：（1）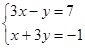
（2）
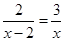
（3）x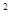
－2x＝2x＋1；
（4）x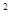﹣3x=0
（5）
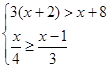
如图，直线l经过点A（1，0），且与双曲线y＝
（x＞0）交于点B（2，1），过点P（p，p－1）（p＞1）作x轴的平行线分别交曲线y＝（x＞0）和y＝－（x＜0）于M，N两点．
（1）求m的值及直线l的解析式；
（2）若点P在直线y＝2上，求证：△PMB∽△PNA；
（3）是否存在实数p，使得S△AMN＝4S△APM？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．