已知:如图,抛物线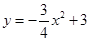 与
与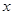 轴交于点
轴交于点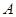 ,点
,点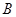 ,与直线
,与直线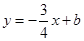 相交于点
相交于点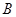 ,点
,点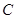 ,直线
,直线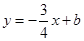 与
与 轴交于点
轴交于点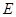 .
.
(1)求
 的面积.
的面积.(2)若点
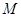 在线段
在线段 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从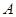 向
向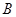 运动(不与
运动(不与 重合),同时,点
重合),同时,点 在射线
在射线 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从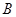 向
向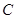 运动.设运动时间为
运动.设运动时间为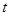 秒,请写出
秒,请写出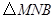 的面积
的面积 与
与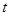 的函数关系式,并求出点
的函数关系式,并求出点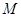 运动多少时间时,
运动多少时间时,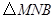 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
某初中数学老师要从甲乙两位学生中选一名参加数学竞赛,甲乙两人前5学期的数学成绩如下表,
(1)分别求出甲乙二人前五学期的数学平均成绩.
(2)在下图中分别画出甲、乙前五学期数学成绩折线图.
(3)如果你是老师,你认为该选哪位学生参加数学竞赛?请简要说明理由.
某部门为了给员工普及电脑知识,决定购买A、B两种电脑,A型电脑单价为4800元,B型电脑单价为3200元,若用不超过160000元去购买A、B型电脑共36台,要求购买A型电脑多于25台,有哪几种购买方案?
先化简下列式子,再从2,﹣2,1,0,﹣1中选择一个合适的数进行计算.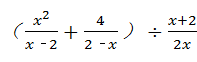 .
.
一场特大暴雨造成遂渝高速公路某一路段被严重破坏。为抢修一段120米长的高速公路,施工队每天比原计划多修5米,结果提前4天完成抢修任务。问原计划每天抢修多少米?
如图:抛物线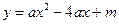 与x 轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C。
与x 轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C。
⑴求抛物线的对称轴和点B的坐标;
⑵过点C作CP⊥对称轴于点P,连结BC交对称轴于点D,连结AC、BP,且 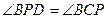 ,求
,求 抛物线的解析式;
抛物线的解析式;
⑶在⑵的条件下,设抛物线的顶点为G,连结BG、CG、求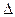 BCG的面积。
BCG的面积。