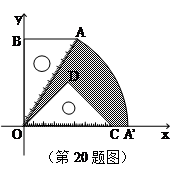
如图,有一块含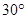 的直角三角板
的直角三角板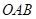 的直角边长
的直角边长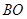 的长恰与另一块等腰直角三角板
的长恰与另一块等腰直角三角板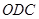 的斜边
的斜边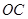 的长相等,把该套三角板放置在平面直角坐标系中,且
的长相等,把该套三角板放置在平面直角坐标系中,且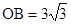 .
.若双曲线的一个分支恰好经过点
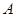 ,求双曲线的解析式;
,求双曲线的解析式;若把含
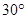 的直角三角板绕点
的直角三角板绕点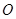 按顺时针方向旋转后,斜边
按顺时针方向旋转后,斜边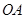 恰好与
恰好与 轴重叠,点
轴重叠,点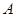 落在点
落在点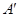 ,试求图中阴影部分的面积(结果保留
,试求图中阴影部分的面积(结果保留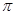 ).
).
数学老师到菜市场买菜,发现若把10千克的菜放在某秤上,秤的指针盘上的指针转了180°,于是老师在学完一元一次方程和角的相关知识后给学生提出了两个问题:
(1)老师把6千克的菜放在该秤上,指针转过多少度?
(2)若刘大妈第一次把若干千克的菜放在秤上,通过指针盘度数发现与自己所需数量还差一些,于是再放了1千克的菜上去,发现前、后两次指针转过的角度恰好互余.求刘大妈第一次放多少千克菜在秤盘上?
如图,AB与CD相交于O点,∠1=50°,则∠2=.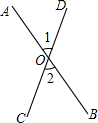
如图,直线AB与CD相交于O,OE平分∠AOB,OF平分∠COD.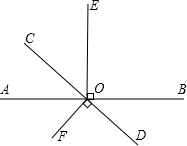
(1)图中与∠COA互补的角是;(把符合条件的所有角都写出来)
(2)如果∠AOC=35°,求∠EOF的度数.
以下两题请选择一题解答,若两题都答,只把第1题的分数记入学分.
①如图1,已知射线OC在平角∠AOB的内部,且∠AOC>∠BOC,OD平分∠AOC,OE平分∠BOC.
(1)比较∠COD与∠COE的大小,并说明理由.
(2)你能求出∠DOE的大小吗?如果能,请求出它的度数,若不能,说明理由.
(3)若∠AOB=a,你能用a表示∠DOE的度数吗?请说明理由.
②如图2,∠AOC与∠BOD都是直角,∠BOC=50°.
(1)求∠AOB和∠DOC的度数,∠AOB和∠DOC有何大小关系?
(2)若∠BOC的具体度数不稳定,其他条件不变,这种关系仍然成立吗?说明理由.
(3)试猜想∠AOD与∠COB在数量上是相等、互余,还是互补关系?你能用推理的方法说明你的猜想是否合理吗?
(4)当∠BOD绕点O旋转到图3位置时,你原来的猜想还成立吗?说明理由.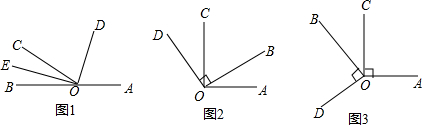
如图,OA⊥OC.OB⊥OD,∠1=50°,求∠2的度数.