如图1，正方形ABCD和正方形QMNP，∠M =∠B，M是正方形ABCD的对称中心，MN交AB于F，QM交AD于E．求证：ME = MF．
如图2，若将原题中的“正方形”改为“菱形”，其他条件不变，探索线段ME与线段MF的关系，并加以证明．
如图3，若将原题中的“正方形”改为“矩形”，且AB = mBC，其他条件不变，探索线段ME与线段MF的关系，并说明理由．
根据前面的探索和图4，你能否将本题推广到一般的平行四边形情况？若能，写出推广命题；若不能，请说明理由．
推理填空，如图
1、如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE.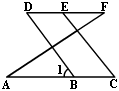
解：∵∠A=∠F(已知)
∴AC∥DF()
∴∠D=∠( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
作图题（尺规作图，不写作法，但保留作图痕迹）
如图，已知，∠α 、∠β。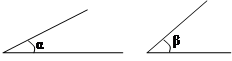
求作∠AOB,使∠AOB =2∠α+∠β，
先化简，再求值：
，其中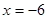
正方形ABCD中，E点为BC中点，连接AE，过B点作BF⊥AE，交CD于F点，交AE于G点，连接GD，过A点作AH⊥GD交GD于H点．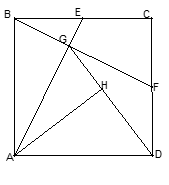
(1) 求证：△ABE≌△BCF；
(2) 若正方形边长为4，AH =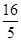
，求△AGD的面积．
如图，直角梯形ABCD中，AD∥BC，∠A＝90°，AB＝AD＝6，DE⊥DC交AB于E，DF平分∠EDC交BC于F，连接EF．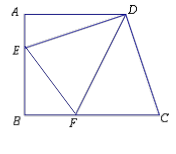
（1） 证明：EF＝CF；
(2) 当AE＝2时，求EF的长．