(1) 在图1中,已知点E,F分别为线段AB,CD的中点.

② A (-1,0), B (3,0),则E点坐标为__________;
②若C (-2,2), D (-2,-1),则F点坐 标为__________;
标为__________;(2)若已知线段AB的端点坐标为A (1,3), B (5,1)则线段AB的中点D的坐标为 ;
(3)在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),则线段AB的中点D的坐标为 .(用含a,b,c,d的代数式表示).

归纳:无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d),AB中点为D(x,y) 时,x =_________,
=_________, y=___________.(不必证明)
y=___________.(不必证明)
●运用:在图2中,一次函数 与反比例函数
与反比例函数 的图象交点为A,B.
的图象交点为A,B.
①求出交点A,B的坐标;
②若以A,O,B,P为顶点的四边形是平行四边形,请利用上面的结论求出顶点P的坐标.
已知2 -x-2=0,求
-x-2=0,求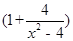 ·(x-2)的值
·(x-2)的值
化简下列分式
(1)、 (2)、
(2)、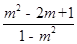
如图,在△ABC中,AB=AC,D,E分别是AC,AB上的点,且BC=BD,AD=DE=EB,∠A度数是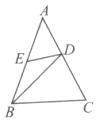
| A.30° | B.45° | C.50° | D.60° |
如图,抛物线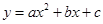 (
( )与x轴相交于两点E、B(E在B的左侧),与y轴相交于点C(0,2),点D的坐标为(-4,0),且AB=AE=2,
)与x轴相交于两点E、B(E在B的左侧),与y轴相交于点C(0,2),点D的坐标为(-4,0),且AB=AE=2,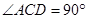 .
.
(1)求点A、B、E的坐标;
(2)求抛物线的解析式;
(3)在第一象限的抛物线上,是否存在一点M,作MN⊥x轴,垂足为N,使得以M、N、O为顶点的三角形与△AOC相似.
如图,△ 为一锐角三角形,
为一锐角三角形, ,
, 边上的高
边上的高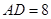 .点
.点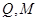 在边
在边 上,
上,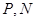 分别在边
分别在边 上,且
上,且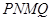 为矩形.
为矩形.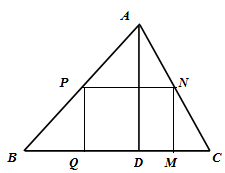
(1)设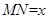 ,用
,用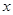 表示
表示 的长度;
的长度;
(2)当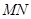 长度为多少时,矩形
长度为多少时,矩形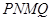 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
(3)当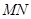 长度为多少时,△
长度为多少时,△ 的面积等于△
的面积等于△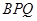 与△
与△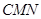 之和?
之和?