已知正方形纸片ABCD.如图1,将正方形纸片折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.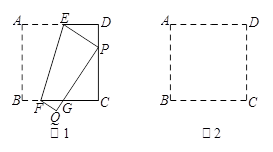
(1)请你找到一个与
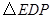 相似的三角形,并证明你的结论;
相似的三角形,并证明你的结论;(2)当AB=2,点P位于CD中点时,请借助图2画出折叠后的示意图,并求CG的长.
如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB为⊙O上关于A、B的滑动角。
(1)已知∠APB是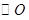 上关于点A、B的滑动角。
上关于点A、B的滑动角。
① 若AB为⊙O的直径,则∠APB=
② 若⊙O半径为1,AB= ,求∠APB的度数
,求∠APB的度数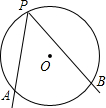
(2)已知 为
为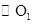 外一点,以
外一点,以 为圆心作一个圆与
为圆心作一个圆与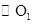 相交于A、B两点,∠APB为
相交于A、B两点,∠APB为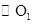 上关于点A、B的滑动角,直线PA、PB分别交
上关于点A、B的滑动角,直线PA、PB分别交 于点M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系。
于点M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系。
“?”的思考
下框中是小明对一道题目的解答以及老师的批阅。
 |
我的结果也正确
小明发现他解答的结果是正确的,但是老师却在他的解答中划了一条横线,并打开了一个“?”
结果为何正确呢?
(1)请指出小明解答中存在的问题,并补充缺少的过程:
变化一下会怎样……
(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.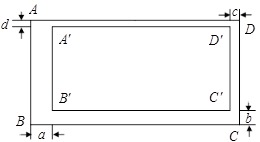
某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售有如下关系,若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售一部,所有出售的汽车的进价均降低0.1万元/部。月底厂家根据销售量一次性返利给销售公司,销售量在10部以内,含10部,每部返利0.5万元,销售量在10部以上,每部返利1万元。
① 若该公司当月卖出3部汽车,则每部汽车的进价为万元;
② 如果汽车的销售价位28万元/部,该公司计划当月盈利12万元,那么要卖出多少部汽车?(盈利=销售利润+返利)
某玩具由一个圆形区域和一个扇形区域组成,如图,在 和扇形
和扇形 中,
中, 与
与 、
、 分别相切于A、B,
分别相切于A、B,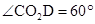 ,E、F事直线
,E、F事直线 与
与 、扇形
、扇形 的两个交点,EF=24cm,设
的两个交点,EF=24cm,设 的半径为x cm,
的半径为x cm,
① 用含x的代数式表示扇形 的半径;
的半径;
② 若 和扇形
和扇形 两个区域的制作成本分别为0.45元
两个区域的制作成本分别为0.45元 和0.06元
和0.06元 ,当
,当 的半径为多少时,该玩具成本最小?
的半径为多少时,该玩具成本最小?
看图说故事。
请你编一个故事,使故事情境中出现的一对变量x、y满足图示的函数关系式,要求:①指出x和y的含义;②利用图中数据说明这对变量变化过程的实际意义,其中需设计“速度”这个量