认真阅读下面关于三角形内外角平分线所夹的探究片段，完成所提出的问题.
探究如图11-1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+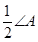
,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线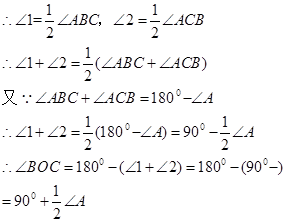
如图11-2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由.
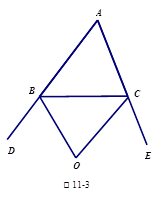
如图11-3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（只写结论，不需证明）
结论： .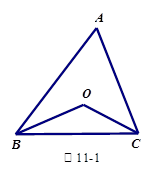
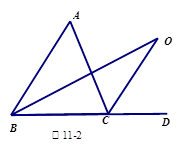
一根蜡烛高20cm，蜡烛高度 y（单位：cm）随燃烧的时间x（单位：分钟）的增加而减少，平均每分钟减少量为0．1cm/分钟．求y与x的函数关系式，并画出该函数的图象．
如图，在平行四边形ABCD中，E是BC边上的点，且BE=3EC，AE与DC的延长线交于点F．若CD=6，求CF的长．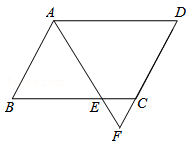
已知：如图，在四边形ABCD中，∠A=130°，∠C=90°，∠D=40°，BE∥AD交CD于点E．求证：BE平分∠ABC．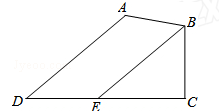
一个不透明的口袋中有3个完全相同的小球，分别标有数字1，2，3，随机摸出一个小球然后放回，再随机摸出一个小球，求两次摸出的小球数字之积等于3的概率．
如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（-1，3），B（-3，2），C（0，1）．画出△ABC，并画出关于原点O对称的△A1B1C1．