(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处,极轴与 轴的正半轴重合,曲线C1
轴的正半轴重合,曲线C1 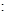
 (t为参数),曲线
(t为参数),曲线 .
.
(Ⅰ)写出C1与C2的普通方程;
(Ⅱ)过坐标原点O做C1的垂线,垂足为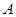 ,P为OA中点,当
,P为OA中点,当 变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
(本小题满分14分) 
已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,
PA⊥平面ABCD.
(1)求证:PF⊥FD;
(2)设点G在PA上,且EG//平面PFD,试确定点G的位置.
(本小题满分12分)
四个大小相同的小球分别标有数字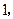
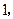
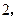
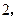 把它们放在一个盒子中,从中任意摸出两个小球,它们的标号分别为
把它们放在一个盒子中,从中任意摸出两个小球,它们的标号分别为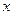 、
、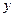 ,记随机变量
,记随机变量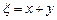 .
.
(1)求随机变量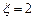 时的概率;
时的概率;
(2)求随机变量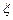 的概率分布列及数学期望。
的概率分布列及数学期望。
(本小题满分12分)
已知向量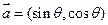 与
与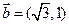 ,其中
,其中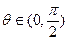
(1)若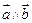 ,求
,求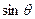 和
和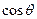 的值;
的值;
(2)若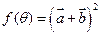 ,求
,求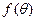 的值域。
的值域。

已知定点A(-2,0),动点B是圆 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.
(1)求动点P的轨迹方程;
|
(2)是否存在过点E(0,-4)的直线l交P点的轨迹于点R,T,且满足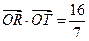 (O为原点).若存在,求直线l的方程;若不存在,请说明理由.
(O为原点).若存在,求直线l的方程;若不存在,请说明理由.
已知数列 中,
中, 且点
且点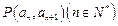 在直线
在直线 上.
上.
(1)求数列 的通项公式;
的通项公式;
(2)若函数 求函数
求函数 的最小值;
的最小值;
(3)设 表示数列
表示数列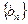 的前
的前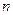 项和,
项和,
试证明: .
.