(本小题满分16分)已知函数f(x)=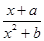 是定义在R上的奇函数,其值域为
是定义在R上的奇函数,其值域为 .
.
(1) 试求a、b的值;
(2) 函数y=g(x)(x∈R)满足:
条件1: 当x∈[0,3)时,g(x)=f(x);条件2: g(x+3)=g(x)lnm(m≠1).
① 求函数g(x)在x∈[3,9) 上的解析式;
上的解析式;
② 若函数g(x)在x∈[0,+∞)上的值域是闭区间,试探求m的取值范围,并说明理由.
(本小题满分15分)已知函数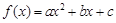 (
( 且
且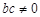 ).
).
(Ⅰ)若 ,试求
,试求 的解析式;
的解析式;
(Ⅱ)令 ,若
,若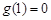 ,又
,又 的图像在
的图像在 轴上截得的弦的长度为
轴上截得的弦的长度为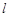 ,且
,且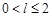 ,试比较
,试比较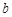 、
、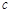 的大小.
的大小.
(本小题满分14分)如图, 中,
中, ,四边形
,四边形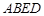 是矩形,
是矩形, ,平面
,平面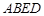
 平面
平面 ,
, 、
、 分别是
分别是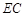 、
、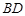 的中点,
的中点,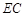 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.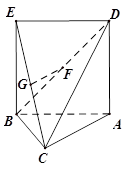
(Ⅰ)求证: ∥底面
∥底面 ;
;
(Ⅱ)求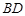 与面
与面 的所成角.
的所成角.
(本小题满分14分)设数列 的首项
的首项 ,前
,前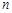 项和为
项和为 ,且满足
,且满足
 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)求证: .
.
(本小题满分14分)已知函数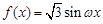
 的部分图像如图所示.
的部分图像如图所示. 、
、 分别是图像上的一个最高点和最低点,
分别是图像上的一个最高点和最低点, 为图像与
为图像与 轴的交点,且四边形
轴的交点,且四边形 为矩形.
为矩形.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)将 的图像向右平移
的图像向右平移 个单位长度后,得到函数
个单位长度后,得到函数 的图像.已知
的图像.已知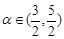 ,
, ,求
,求 的值.
的值.
(本小题满分14分)已知函数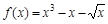 .
.
(1)判断 的单调性;
的单调性;
(2)求函数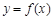 的零点的个数;
的零点的个数;
(3)令 ,若函数
,若函数 在
在 内有极值,求实数a的取值范围.
内有极值,求实数a的取值范围.