某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为 第二、第三门课程取得优秀成绩的概率分别为
第二、第三门课程取得优秀成绩的概率分别为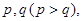 且不同课程是否取得优秀成绩相互独立,记
且不同课程是否取得优秀成绩相互独立,记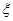 为该生取得优秀成绩的课程数,其分布列为
为该生取得优秀成绩的课程数,其分布列为
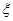 |
0 |
1 |
2 |
3 |
 |
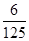 |
 |
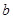 |
 |
(1)求该生至少有1门课程取得优秀成绩的概率;
(2)求 ,
,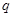 的值;
的值;
(3)求数学期望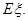
如图,已知长方形 中,
中, ,
,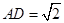 ,
,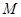 为
为 的中点.将
的中点.将 沿
沿 折起,使得平面
折起,使得平面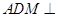 平面
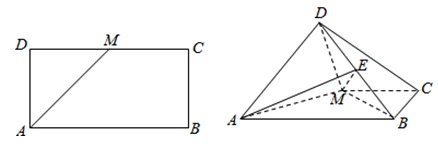
平面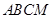 .
.
(1)求证: ;
;
(2)若点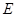 是线段
是线段 上的一动点,问点
上的一动点,问点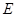 在何位置时,二面角
在何位置时,二面角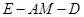 的余弦值为
的余弦值为 .
.
如图, 中,三个内角
中,三个内角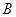 、
、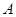 、
、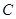 成等差数列,且
成等差数列,且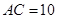 ,
,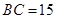 .
.
(1)求 的面积;
的面积;
(2)已知平面直角坐标系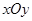 ,点
,点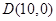 ,若函数
,若函数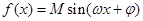
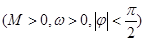 的图象经过
的图象经过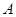 、
、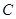 、
、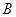 三点,且
三点,且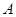 、
、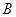 为
为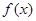 的图象与
的图象与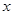 轴相邻的两个交点,求
轴相邻的两个交点,求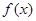 的解析式.
的解析式.
在等比数列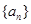 中,
中,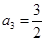 ,
,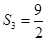 .
.
(1)求数列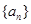 的通项公式;
的通项公式;
(2)设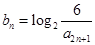 ,且
,且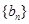 为递增数列,若
为递增数列,若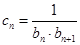 ,求证:
,求证: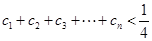 .
.
已知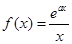 ,(
,(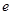 为自然对数的底数).
为自然对数的底数).
(Ⅰ)若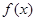 在
在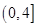 上是减函数,求实数
上是减函数,求实数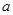 的取值范围;
的取值范围;
(Ⅱ)当 时,求函数
时,求函数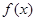 在
在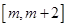 (
(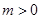 )上的最小值;
)上的最小值;
(Ⅲ)求证: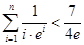 .
.
设数列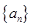 的前
的前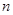 项和为
项和为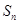 ,已知
,已知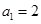 ,
,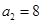 ,
,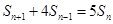 (
(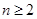 ),
),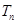 是数列
是数列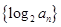 的前
的前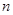 项和.
项和.
(1)求数列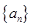 的通项公式;
的通项公式;
(2)求满足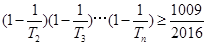 的最大正整数
的最大正整数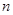 的值.
的值.