设函数 在
在 及
及 时取得极值.
时取得极值.
(Ⅰ)求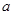 、
、 的值;
的值;
(Ⅱ)若对于任意的 ,都有
,都有 成立,求c的取值范围
成立,求c的取值范围
(本小题满分10分) 已知A={x|x2-ax+a2-19=0},B={x|x2-5x+8=2},C={x|x2+2x-8=0}.若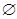
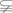 A∩B,且A∩C=
A∩B,且A∩C=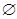 ,求a的值.
,求a的值.
(本小题满分10分)已知集合A={2,4,a3-2a2-a+7},B={-4,a+3,a2-2a+2,a3+a2+3a+7},若A∩B={2,5},求实数a的值,并求A∪B.
设A={x|x2+(a+2)x+a+1=0},求A中所有元素之和.
说明集合A={x|y=x2+1},B={y|y=x2+1},C={(x,y)|y=x2+1}的区别.
设函数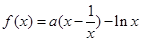
(1)当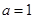 时,求曲线
时,求曲线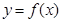 在点
在点 处的切线方程;
处的切线方程;
(2)若函数 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数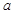 的取值范围;
的取值范围;
(3)设函数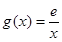 ,若在
,若在 上至少存在一点
上至少存在一点 使
使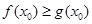 成立,求实数
成立,求实数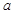 的取值范围.
的取值范围.