已知数列 中,
中,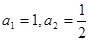 且数列
且数列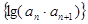 的前n项和
的前n项和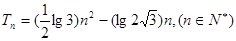 又设
又设 。
。
(Ⅰ)求证:数列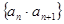 是等比数列;
是等比数列;
(II)求数列 的通项
的通项 及前n项和
及前n项和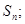
(III)求证: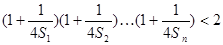
已知等差数列 的前n项和为
的前n项和为 ,
, 。
。
(1)求 的通项
的通项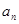 ;
;
(2)数列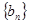 为等比数列,
为等比数列,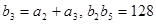 ,求
,求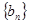 的前8项和
的前8项和 。
。
已知 ,
,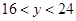 ,分别求
,分别求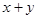 、
、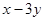 及
及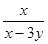 的范围。
的范围。
已知焦点在 轴,顶点在原点的抛物线
轴,顶点在原点的抛物线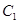 经过点P(2,2),以
经过点P(2,2),以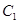 上一点
上一点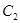 为圆心的圆过定点
为圆心的圆过定点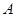 (0,1),记
(0,1),记 为圆
为圆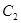 与
与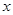 轴的两个交点.
轴的两个交点.
(1)求抛物线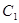 的方程;
的方程;
(2)当圆心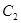 在抛物线上运动时,试判断
在抛物线上运动时,试判断 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心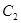 在抛物线上运动时,记
在抛物线上运动时,记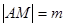 ,
,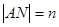 ,求
,求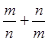 的最大值.
的最大值.
已知函数 .
.
(1)若 ,解方程
,解方程 ;
;
(2)若函数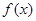 在
在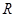 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(3)若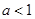 且不等式
且不等式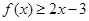 对一切实数
对一切实数 恒成立,求
恒成立,求 的取值范围
的取值范围
如图,在直三棱柱 中,
中, 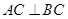 ,
,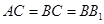 ,点
,点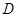 是
是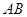 的中点,
的中点,
(1)求证: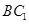 ∥平面
∥平面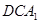 ;
;
(2)设点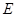 在线段
在线段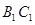 上,
上,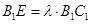 ,且使直线
,且使直线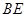 和平面
和平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求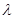 的值.
的值.