如图,在三棱锥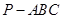 中,
中,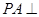 底面ABC
底面ABC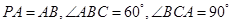 ,点
,点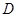 、
、 分别在棱
分别在棱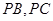 上,且
上,且 http://wx.jtyjy.com/
http://wx.jtyjy.com/
(Ⅰ)求证: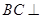 平面
平面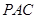 ;
;
(Ⅱ)当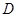 为
为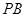 的中点时,求
的中点时,求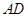 与平面
与平面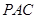 所成角的大小的余弦值;
所成角的大小的余弦值;
(Ⅲ)是否存在点 ,使得二面角
,使得二面角 为直二面角?并说明理由.
为直二面角?并说明理由.
本小题满分8分)
已知函数 。
。
(1)作出函数 的图象,(2)证明:函数
的图象,(2)证明:函数 在
在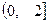 上是增函数
上是增函数
(本小题满分8分)(1)不查表计算 +
+ ;
;
(2)解方程: 。
。
(本小题满分8分)某商品在近30天内每件的销售价格 (元)与时间
(元)与时间 天的函数关系是
天的函数关系是 该商品的日销售量
该商品的日销售量 (件)与时间
(件)与时间 (天)的函数关系是
(天)的函数关系是 (1),求这种商品的日销售额
(1),求这种商品的日销售额 的解析式,(2)求
的解析式,(2)求 的最大值.并指出日销售额的最大时是30天中的第几天
的最大值.并指出日销售额的最大时是30天中的第几天
21. (本小题满分12分)
已知函数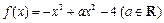 .
.
(1)若函数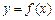 的图象在点P(1,
的图象在点P(1, )处的切线的倾斜角为
)处的切线的倾斜角为 ,求实数a的值;
,求实数a的值;
(2)设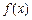 的导函数是
的导函数是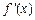 ,在 (1) 的条件下,若
,在 (1) 的条件下,若 ,求
,求 的最小值.
的最小值.
(3)若存在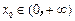 ,使
,使 ,求a的取值范围.
,求a的取值范围.
20. (本小题满分12分)
已知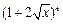 的展开式中,某一项的系数是它前一项系数的2倍,而等于它后一项的系数的
的展开式中,某一项的系数是它前一项系数的2倍,而等于它后一项的系数的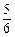 .
.
(1)求该展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.