(本小题满分12分)
某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作。比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。
假设每个运动员完成每个系列中的K和D两个动作的得分是相互独立的。根据赛前训练的统计数据,某运动员完成甲系列和乙系列中的K和D两个动作的情况如下表:
表1:甲系列表2:乙系列
| 动作 |
K动作 |
D动作 |
||
| 得分 |
100 |
80 |
40 |
10 |
| 概率 |
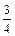 |
 |
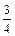 |
 |
| 动作 |
K动作 |
D动作 |
||
| 得分 |
90 |
50 |
20 |
0 |
| 概率 |
 |
 |
 |
 |
现该运动员最后一个出场,之前其他运动员的最高得分为115分。
(1)若该运动员希望获得该项目的第一名,应选择哪个系列?说明理由。
并求其获得第一名的概率。
(2) 若该运动员选择乙系列,求其成绩 的分布列及数学期望
的分布列及数学期望
(本小题满分12分)(注意:在试题卷上作答无效)
在平面直角坐标系 中,已知直线
中,已知直线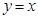 与圆心在第二象限的圆
与圆心在第二象限的圆 相切于原点
相切于原点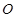 ,且圆
,且圆 与圆
与圆
 的面积相等.
的面积相等.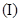 求圆
求圆 的标准方程;
的标准方程; 试探究圆
试探究圆 上是否存在异于原点的点
上是否存在异于原点的点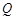 ,使点
,使点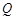 到定点
到定点 的距离等于线段
的距离等于线段 的长?若存在,求出点
的长?若存在,求出点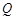 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分12分)(注意:在试题卷上作答无效)
在平面直角坐标系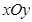 中,已知
中,已知 ,
, .
. 若
若 ∥
∥ ,求
,求 的坐标;
的坐标; 若
若 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角 的大小.
的大小.
(本小题满分12分)(注意:在试题卷上作答无效)
已知函数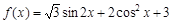 .
. 求
求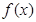 的最小正周期;
的最小正周期;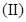 求
求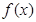 在
在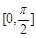 上的最值.
上的最值.
(本小题满分10分)(注意:在试题卷上作答无效)
在锐角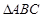 中,角
中,角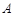 、
、 、
、 的对边分别为
的对边分别为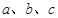 ,且
,且 .
. 求角
求角 的大小;
的大小; 若
若 ,求
,求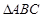 的面积.
的面积.
(本小题满分14分)
设 是函数
是函数 的图象上任意两点,且
的图象上任意两点,且 ,已知点
,已知点 的横坐标为
的横坐标为 .
.
(1)求证: 点的纵坐标为定值;
点的纵坐标为定值;
(2)若 求
求 ;
;
(3)已知 =
= ,其中
,其中 ,
, 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切 都成立,试求
都成立,试求 的取值范围.
的取值范围.