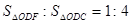(本小题满分15分)已知椭圆C: +
+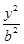 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为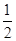 ,且经过点P(1,
,且经过点P(1,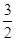 ).
).
(1)求椭圆C的方程;
(2)设F是椭圆C的右焦点,M为椭圆上一点,以M为圆心,MF为半径作圆M.问点M满足什么条件时,圆M与y轴有两个交点? 并求两点间距离的最大值.
在△ABC中,已知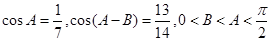
(1)求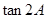 的值;(2)求角
的值;(2)求角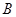
已知函数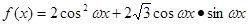 ,(其中
,(其中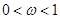 ),若直线
),若直线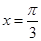 是函数
是函数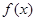 图象的一条对称轴。
图象的一条对称轴。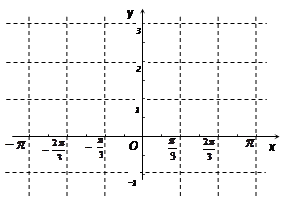
(1)试求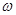 的值;
的值;
(2)先列表再作出函数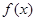 在区间
在区间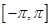 上的图象.
上的图象.
选修4-5:不等式选讲
设不等式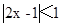 的解集为
的解集为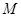 .
.
(1)求集合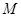 ;
;
(2)若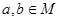 ,试比较
,试比较 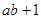 与
与 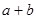 的大小.
的大小.
选修4-4:坐标系与参数方程
在直角坐标系 中,直线L的方程为x-y+4=0,曲线C的参数方程为
中,直线L的方程为x-y+4=0,曲线C的参数方程为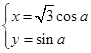
(1)求曲线C的普通方程;
(2)设点Q是曲线C上的一个动点,求它到直线L的距离的最小值.
选修4-1:几何证明选讲
如图,在等腰梯形ABCD中,对角线AC⊥BD,且相交于点O ,E是AB边的中点,EO的延长线交CD于F.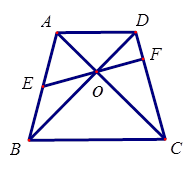
(1)求证:EF⊥CD;
(2)若∠ABD=30°,求证