一个盒子中装有5张卡片，每张卡片上写有一个数字，数字分别是1、2、3、4、5，现从盒子中随机抽取卡片。
（1）从盒中依次抽取两次卡片，每次抽取一张，取出的卡片不放回，求两次取到的卡片的数字既不全是奇数，也不全是偶数的概率；
（2）若从盒子中有放回的抽取3次卡片，每次抽取一张，求恰有两次取到卡片的数字为偶数的概率；
（3）从盒子中依次抽取卡片，每次抽取一张，取出的卡片不放回，当放回记有奇数的卡片即停止抽取，否则继续抽取卡片，求抽取次数X的分布列和期望。
（本小题满分16分）已知函数
的图像过点
，且在
处的切线的斜率为
，（为正整数）
（Ⅰ）求函数
的解析式；
（Ⅱ）若数列
满足：
，
，令
，求数列
的通项公式；
（Ⅲ）对于（Ⅱ）中的数列
，令
，求数列
的前项的和
．
（本小题满分16分）已知奇函数
的定义域为
，当
时，
．
（1）求函数在
上的值域；
（2）若
，y=
的最小值为
，求实数
的值．
（本小题满分14分）某旅游景点预计2014年1月份起前x个月的旅游人数的和p（x）（单位：万人）与x的关系近似满足
，已知第x月的人均消费额q（x）（单位：元）与x的近似关系是 q（x）=
（1）写出2014年第x月的旅游人数f（x）（单位：万人）与x的函数关系式；
（2）试问2014年哪个月的旅游消费总额最大，最大旅游消费额为多少万元？
（本小题满分14分）设锐角三角形ABC的内角A，B，C的对边分别为
，
（Ⅰ）求B的大小；
（Ⅱ）求
的取值范围
（本小题满分14分）已知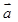向量
=（
，1），向量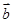
=（sin2x，cos2x），函数
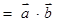
（1）求函数的表达式，并作出函数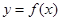
在一个周期内的简图（用五点法列表描点）；
（2）求函数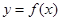的周期，并写单调区间．