(本小题满分15分)
如图,已知四棱锥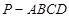 中,平面
中,平面 平面
平面 ,平面
,平面 平面
平面 ,
, 为
为 上任意一点,
上任意一点, 为菱形
为菱形 对角线的交点.
对角线的交点.
(Ⅰ)证明:平面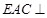 平面
平面 ;
;
(Ⅱ)若 ,三棱锥
,三棱锥 的体积是四棱锥
的体积是四棱锥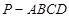 的体积的
的体积的 ,二面角
,二面角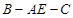 的大小为
的大小为 ,求
,求

用一张长为8 cm,宽为4 cm的矩形硬纸卷成圆柱的侧面,求圆柱的轴截面的面积与底面积.
一个圆锥的高为2 cm,母线与轴的夹角为30°,求圆锥的母线长以及圆锥的轴截面的面积.
正六棱柱各棱长均为1,求一动点从A沿表面移动到点D1时最短的路程.
如右图所示,在正三棱柱ABC—A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为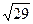 ,设这条最短路线与CC1的交点为N.求:
,设这条最短路线与CC1的交点为N.求: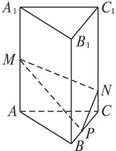
(1)该三棱柱的侧面展开图的对角线长;
(2)PC和NC的长.
长方体ABCD—A1B1C1D1(如右图所示),宽、长、高分别为3、4、5,现有一甲壳虫从A出发沿长方体表面爬行到C1来获取食物,试画出它的最短爬行路线,并求其路程的最小值.