（1）求与双曲线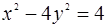
有共同的渐近线，且过点
的双曲线的方程。
（2）已知中心在原点，一焦点为F（0，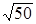
）的椭圆被直线L：y=3x-2截得的弦的中点的横坐标为
，求此椭圆的方程。
某校10名学生组成该校“科技创新周”志愿服务队（简称“科服队”），他们参加活动的有关数据统计如下：
| 参加活动次数 |
1 |
2 |
3 |
| 人 数 |
2 |
3 |
5 |
（1）从“科服队”中任选3人，求这3人参加活动次数各不相同的概率；
（2）从“科服队”中任选2人，用
表示这2人参加活动次数之差的绝对值，求随机变量的分布列及数学期望
．
已知矩形
内接于圆柱下底面的圆
，
是圆柱的母线，若
，
，此圆柱的体积为
，求异面直线
与
所成角的余弦值．
已知函数f(x) =2lnx-x2
(I)若方程
在[
，e]内有两个不等的实根，求实数m的取值范围（e为自然对数的底数）；
(II)如果函数，
的图象与-轴交于两点力（
),B(
)，且
求证：
（其中
为
的导函数).
已知线段AB的两个端点A，B分别在x轴、y轴上滑动，|AB|=3，点M满足
(I)求动点M的轨迹E的方程；
(II )若曲线E的所有弦都不能被直线y=k(x-1)垂直平分,求实数k的取值范围.
在数列
中，
（其中
为数列
的前n项和).
(I )求数列
的通项公式
；
(II)若
，求数列
的前n项和
，