如图,已知:AC⊥AB,BD⊥AB,且AC=BE,AE=BD,求证:△CDE是等腰直角三角形;
证明:∵AC⊥AB,BD⊥AB ∴∠CAE=∠DBE=90°
∵AC= BE,AE=BD ∴△ACE≌△BED
∴CE=DE且∠ACE=∠BED
∵∠ACE+∠AEC=90° ∴∠AEC+∠BED=90°
∴∠CED=90° ∴△CED为等腰直角三角形
利用上题的解题思路解答下列问题:
在Rt△ABC中,∠C=90°,D,E分别为CB,CA延长线上的点,BE与AD的交点为P.若BD=AC,AE=CD,在下图中画出符合题意的图形,求出∠APE的度数;
若AC=BD,CD=AE,则∠APE=__________°
解方程:
(1)3x﹣4(2x+5)=x+4;
(2) .
.
计算:
(1)(﹣2)2×7﹣62÷(﹣3)×
(2)先化简,再求值:2(a2b+ab2)﹣2(a2b﹣1)﹣3ab2+2,其中a=﹣2,b=2.
(1)计算:(﹣4a2b4c)÷( a2b3)•2ab2
a2b3)•2ab2
(2)计算: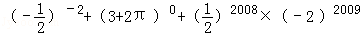
(3)先化简,再求值:[(xy+2)(xy﹣2)﹣2x2y2+4]÷(xy),其中x=10,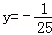 .
.
观察下列各式:
13+23= ;
;
13+23+33=36= ;
;
13+23+33+43=100= ;
;
(1)计算:13+23+33+43+53的值;
(2)计算:13+23+33+43+…+103的值;
(3)猜想:13+23+33+43+…+n3的值.
在下面的集合中选出两个整数和两个分数进行加减混合运算,并使运算结果为整数.