甲、乙两地相距s千米,汽车从甲地匀速行驶到乙地,速度不得超过c千米/小时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/小时)的平方成正比,比例系数为 ,固定部分为a元。
,固定部分为a元。
(1)把全程运输成本y(元)表示为速度v(千米/小时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
(本小题满分12分)
如图,五面体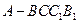 中,
中,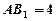 .底面
.底面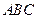 是正三角
是正三角
形,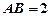 .四边形
.四边形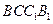 是矩形,二面角
是矩形,二面角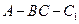 为
为
直二面角.
(Ⅰ)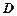 在
在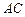 上运动,当
上运动,当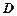 在何处时,有
在何处时,有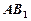 ∥平面
∥平面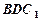 ,
,
并且说明理由;
(Ⅱ)当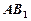 ∥平面
∥平面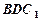 时,求二面角
时,求二面角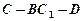 余弦值.
余弦值.
(本小题满分12分)
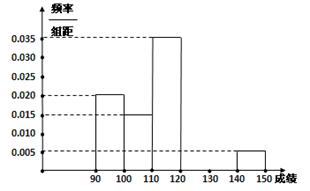
某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六 组,第一组
组,第一组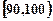 、第二组
、第二组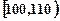 …第六组
…第六组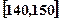 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
(Ⅰ)请补充完整频率分布直方图,并估
计这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第四组和第六组
中任意选2人,记他们的成绩分别
为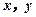 . 若
. 若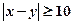 ,则称此二
,则称此二
人为“黄金帮扶组”,试求选出的二
人错误!链接无效。的概率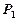 ;
;
(Ⅲ)以此样本的频率当作概率,现随机在这组样本中选出的3名学生,求成绩不低于
120分的人数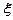 分布列及期望
分布列及期望 .
.
(本小题满分12分)
在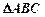 中,角
中,角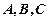 的对边分别为
的对边分别为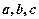 ,且满足
,且满足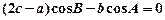
(Ⅰ)若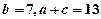 求此三角形的面积;
求此三角形的面积;
(Ⅱ)求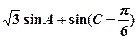 的取值范围.
的取值范围.
(
已知向量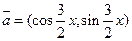 ,
,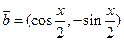 ,且
,且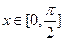
(1)求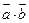 及
及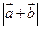 ;
;
(2)求函数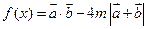
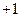 的最小值
的最小值 .
.
(
已知向量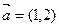 ,
,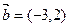 ,向量
,向量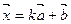 ,
,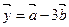 .
. (1)当
(1)当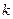 为何值时,向量
为何值时,向量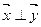 ;
;
(2)若向量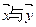 的夹角为钝角,求实数
的夹角为钝角,求实数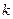 的取值范围.
的取值范围.