(本小题满分12分)
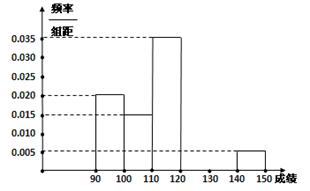
某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六 组,第一组
组,第一组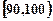 、第二组
、第二组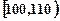 …第六组
…第六组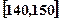 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
(Ⅰ)请补充完整频率分布直方图,并估
计这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第四组和第六组
中任意选2人,记他们的成绩分别
为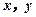 . 若
. 若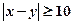 ,则称此二
,则称此二
人为“黄金帮扶组”,试求选出的二
人错误!链接无效。的概率 ;
;
(Ⅲ)以此样本的频率当作概率,现随机在这组样本中选出的3名学生,求成绩不低于
120分的人数 分布列及期望
分布列及期望 .
.
(本小题满分12分)甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为 ,乙投篮命中的概率为
,乙投篮命中的概率为 .
.
(Ⅰ)求甲至多命中2个且乙至少命中 2个的概率;
2个的概率;
(Ⅱ)若规定每投蓝一次命中得3分,未命中得-1分,求乙所得分数 的概率分布和数学期望.
的概率分布和数学期望.
(本小题满分12分)在直角坐标平面内,已知点 ,其中
,其中 .
.
(Ⅰ)若 ,求角
,求角 的弧度数;
的弧度数;
(Ⅱ)若 ,求
,求 的值.
的值.
23.(本小题满分10分)
将一枚硬币连续抛掷 次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为
次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为 ,正面向上的次数为偶数的概率为
,正面向上的次数为偶数的概率为 .
.
(Ⅰ)若该硬币均匀,试求 与
与 ;
;
(Ⅱ)若该硬币有暇疵,且每次正面向上的概率为 ,试比较
,试比较 与
与 的大小.
的大小.
22.(本小题满分10分)
已知动圆 过点
过点 且与直线
且与直线 相切.
相切.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作一条直线交轨迹
作一条直线交轨迹 于
于 两点,轨迹
两点,轨迹 在
在 两点处的切线相交于点
两点处的切线相交于点 ,
, 为线段
为线段 的中点,求证:
的中点,求证: 轴.
轴.
(选修4—5:不等式选讲)
求函数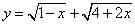 最大值.
最大值.