22.(本小题满分10分)
已知动圆 过点
过点 且与直线
且与直线 相切.
相切.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作一条直线交轨迹
作一条直线交轨迹 于
于 两点,轨迹
两点,轨迹 在
在 两点处的切线相交于点
两点处的切线相交于点 ,
, 为线段
为线段 的中点,求证:
的中点,求证: 轴.
轴.
已知集合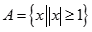 ,函数
,函数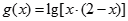 的定义域为
的定义域为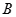 .
.
(1)求集合 .
.
(2)求 .
.
已知函数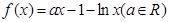 .
.
(1)当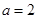 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若函数 在
在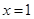 处取得极值,对
处取得极值,对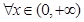 ,
, 恒成立,求实数
恒成立,求实数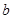 的取值范围;
的取值范围;
(3)当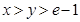 时,求证:
时,求证: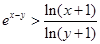 .
.
已知函数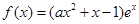 ,其中
,其中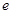 是自然对数的底数,
是自然对数的底数,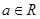 .
.
(1)若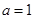 ,求曲线
,求曲线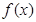 在点
在点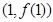 处的切线方程;
处的切线方程;
(2)若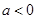 ,求
,求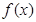 的单调区间;
的单调区间;
(3)若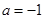 ,函数
,函数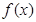 的图像与函数
的图像与函数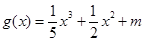 的图像有3个不同的交点,求实数
的图像有3个不同的交点,求实数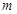 的取值范围.
的取值范围.
已知函数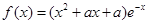 ,(
,( 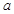 为常数,
为常数,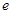 为自然对数的底).
为自然对数的底).
(1)当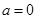 时,求
时,求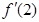 ;
;
(2)若 在
在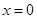 时取得极小值,试确定
时取得极小值,试确定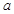 的取值范围;
的取值范围;
(3)在(2)的条件下,设由 的极大值构成的函数为
的极大值构成的函数为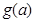 ,将
,将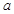 换元为
换元为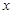 ,试判断曲线
,试判断曲线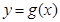 是否能与直线
是否能与直线 (
(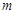 为确定的常数)相切,并说明理由.
为确定的常数)相切,并说明理由.
设函数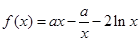 .
.
(1)若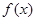 在
在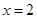 时有极值,求实数
时有极值,求实数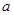 的值和
的值和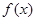 的极大值;
的极大值;
(2)若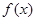 在定义域上是增函数,求实数
在定义域上是增函数,求实数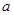 的取值范围.
的取值范围.