(本小题满分12分)
已知函数 ,若x=
,若x= 是
是 的一个极值,且
的一个极值,且 在
在 =1处的切线与直线
=1处的切线与直线 平行。
平行。
(Ⅰ) 求 的解析式及单调区间;
的解析式及单调区间;
(Ⅱ)若对任意的

 都有
都有 ≥
≥ 成立,求函数
成立,求函数 =
= 的最值.
的最值.
(本小题满分12分) 古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n( )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.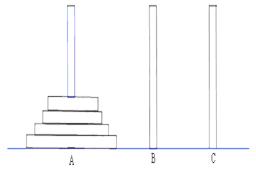
现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
(1)写出a1,a2,a3,并求出an;
(2)记 ,求和
,求和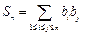 (
( );(其中
);(其中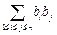 表示所有的积
表示所有的积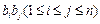 的和)
的和)
(3)证明: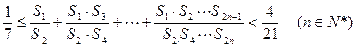
(本小题满分12分)在平面直角坐标系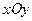 中,线段AB与y轴交于点
中,线段AB与y轴交于点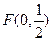 ,直线AB的斜率为k,且满足
,直线AB的斜率为k,且满足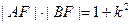
(1)证明:对任意的实数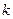 ,一定存在以y轴为对称轴且经过A、B、O三点的抛物线C,并求出抛物线C的方程;
,一定存在以y轴为对称轴且经过A、B、O三点的抛物线C,并求出抛物线C的方程;
(2)对(1)中的抛物线C,若直线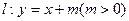 与其交于M、N两点,求∠MON的取值范围.
与其交于M、N两点,求∠MON的取值范围.
(本小题满分12分)如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,……,依次类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第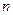 层第
层第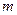 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为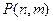 .(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
.(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
(Ⅰ)求 的值,并猜想
的值,并猜想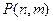 的表达式.(不必证明)
的表达式.(不必证明)
(Ⅱ)设小弹子落入第6层第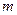 个竖直通道得到分数为
个竖直通道得到分数为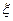 ,其中
,其中 ,试求
,试求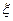 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)如图:直角梯形 中,
中, ,
, 分别为边
分别为边 和
和 上的点,且
上的点,且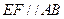 ,
,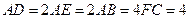 .将四边形
.将四边形 沿
沿 折起成如图2的位置,使
折起成如图2的位置,使 .
.
(Ⅰ)求证:
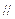 平面
平面 ;
;
(Ⅱ)求三棱锥 的体积;
的体积;
(Ⅲ)求面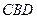 与面
与面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(本小题满分10分)在海岛 上有一座海拔1km的山峰,山顶设有一个观察站
上有一座海拔1km的山峰,山顶设有一个观察站 .有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东
.有一艘轮船按一固定方向做匀速直线航行,上午11:00时,测得此船在岛北偏东 、俯角为
、俯角为 的
的 处,到11:10时,又测得该船在岛北偏西
处,到11:10时,又测得该船在岛北偏西 、俯角为
、俯角为 的
的 处.
处.
(1) 求船的航行速度;
(2) 求船从 到
到 行驶过程中与观察站
行驶过程中与观察站 的最短距离.
的最短距离.