(本小题满分12分)
已知圆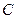 的方程为
的方程为 ,
,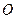 为坐标原点.
为坐标原点.
(Ⅰ)求过点 的圆
的圆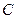 的切线方程;
的切线方程;
(Ⅱ)若圆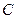 上有两点
上有两点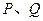 关于直线
关于直线 对称,并且满足
对称,并且满足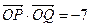 ,求
,求 的值和直线
的值和直线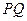 的方程;
的方程;
(Ⅲ)过点 作直线与圆
作直线与圆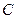 交于
交于 两点,求
两点,求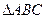 的最大面积以及此时直线
的最大面积以及此时直线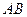 的斜率.
的斜率.
(本小题满分12分)
在四棱锥 中,底面
中,底面 是一直角梯形,
是一直角梯形,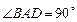 ,
, ,
,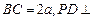 底面
底面 .
.
(1)在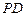 上是否存在一点
上是否存在一点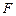 ,使得
,使得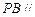 平面
平面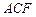 ,若存在,求出
,若存在,求出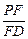 的值;
的值;
若不存在,试说明理由;
(2)在(1)的条件下,若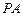 与
与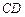 所成的角为
所成的角为 ,求二面角
,求二面角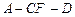 的余弦值.
的余弦值.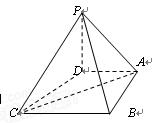
(本小题满分12分)
班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(2)随机抽取8位同学,数学分 数依次为:60,65,70,75,80,85,90,95;
数依次为:60,65,70,75,80,85,90,95;
物理成绩依次为:72,77,80,84,88,90,93,95,
①若规定90分(含90分)以上为优秀,记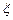 为这8位同学中数学和物理分数均为优秀的人数,求
为这8位同学中数学和物理分数均为优秀的人数,求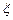 的分布列和数学期望;
的分布列和数学期望;
②若这8位同学的数学、物理分数事实上对应下表:
| 学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
数学分数 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
物理分数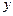 |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据可知,变量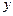 与
与 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出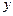 与
与 的线性回归方程(系数精确到0.01).(参考公式:
的线性回归方程(系数精确到0.01).(参考公式: ,其中
,其中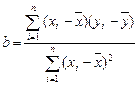 ,
,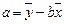 ;参考数据:
;参考数据: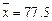 ,
, ,
, ,
,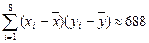 ,
, ,
, ,
,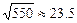 )
)
(本小题满分12分)
“神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预 计到达的区域安排了同一条直线上的三个救援中心(记为
计到达的区域安排了同一条直线上的三个救援中心(记为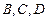 ).当返回舱距地面1万米的
).当返回舱距地面1万米的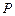 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在 点着陆),
点着陆), 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东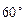 方向,仰角为
方向,仰角为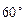 ,
,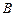 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西 方向,仰角为
方向,仰角为 .
. 救援中心测得着陆点
救援中心测得着陆点 位于其正东方向.
位于其正东方向.
(1)求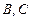
 两救援中心间的距离;
两救援中心间的距离;
(2) 救援中心与着陆点
救援中心与着陆点 间的距离.
间的距离.
已知函数 ,(1)求
,(1)求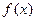 的定义域和值域;
的定义域和值域;
(2)讨论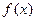 单调性.
单调性.
设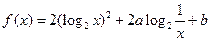 ,已知
,已知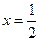 时,
时, 有最小值
有最小值 ,
,
(1)求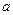 与
与 的值;(2)在(1)的条件下,求
的值;(2)在(1)的条件下,求 的解集
的解集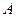 ;
;
(3)设集合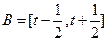 ,且
,且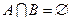 ,求实数
,求实数 的取值范围
的取值范围