为考虑广告费用x与销售额y之间的关系，抽取了5家餐厅，得到如下数据：
| 广告费用(千元) |
1.0 |
4.0 |
6.0 |
10.0 |
14.0 |
| 销售额(千元) |
19.0 |
44.0 |
40.0 |
52.0 |
53.0 |
（1）在同一张图上画散点图，直线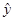
(1)=24＋2.5x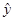，(2)=
；
（2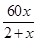）比较所画直线与曲线，哪一条更能表现这组数据之间的关系？
（3）分别计算用直线方程与曲线方程得到在5个x点处的销售额预测值、预测值与实际预测之间的误差，最后比较两个误差绝对值之和的大小。
（本小题满分14分）已知函数
（1）曲线
经过点P（1，2），且曲线C在点P处的切线平行于直线
，求a，b的值；
（2）在（1）的条件下试求函数
的极小值；
（3）若
在区间（1，2）内存在两个极值点，求证：
本小题满分14分）已知
中，点A、B的坐标分别为
，点C在x轴上方。
（1）若点C坐标为
，求以A、B为焦点且经过点C的椭圆的方程；
（2）过点P（m，0）作倾角为
的直线
交（1）中曲线于M、N两点，若点Q（1，0）恰在以线段MN为直径的圆上，求实数m的值。
（本小题满分13分）已知数列
中，
，前n项和为
（1）求数列的通项公式；
（2）设数列
的前n项和为
，求满足不等式
的n值。
（本小题满分12分）某工厂生产一种产品的原材料费为每件40元，若用x表示该厂生产这种产品的总件数，则电力与机器保养等费用为每件0.05x元，又该厂职工工资固定支出12500元。
（1）把每件产品的成本费P（x）（元）表示成产品件数x的函数，并求每件产品的最低成本费；
（2）如果该厂生产的这种产品的数量x不超过3000件，且产品能全部销售，根据市场调查：每件产品的销售价Q（x）与产品件数x有如下关系：
，试问生产多少件产品，总利润最高？（总利润=总销售额-总的成本）
本小题满分12分）已知函数
为偶函数，其图象上相邻的两个最低点间的距离为
。
（1）求
的解析式；
（2）若
，求
的值。