某同学用“五点法”画函数
 在某一个周期的图象时,列表并填入的部分数据如下表:
在某一个周期的图象时,列表并填入的部分数据如下表:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(Ⅰ)求 ,
, ,
, 的值及函数
的值及函数 的表达式;
的表达式; 若对任意的
若对任意的
 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
对于在 上有意义的两个函数
上有意义的两个函数 与
与 ,如果对任意的
,如果对任意的 ,均有
,均有 ,则称
,则称 与
与 在
在 上是接近的,否则称
上是接近的,否则称 与
与 在
在 上是非接近的.现在有两个函数
上是非接近的.现在有两个函数 与
与 ,现给定区间
,现给定区间 .
.
(1)若 ,判断
,判断 与
与 是否在给定区间上接近;
是否在给定区间上接近;
(2)若 与
与 在给定区间
在给定区间 上都有意义,求
上都有意义,求 的取值范围;
的取值范围;
(3)讨论 与
与 在给定区间
在给定区间 上是否是接近的.
上是否是接近的.
已知函数f(x)的定义域是{x|x≠0},对定义域内的任意x1,x2都有f(x1·x2)=f(x1)+f(x2),且当x>1时,f(x)>0,f(2)=1.
(1)证明:f(x)是偶函数;
(2)证明:f(x)在(0,+∞)上是增函数;
(3)解不等式f(2x2-1)<2.
已知函数
 ,函数
,函数 .
.
(1)求函数 与
与 的解析式,并求出
的解析式,并求出 的定义域;
的定义域;
(2)设 ,试求函数
,试求函数 的最值.
的最值.
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: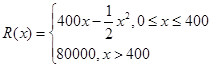 (其中
(其中 是仪器的月产量).
是仪器的月产量).
(1)将利润表示为月产量的函数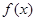 ;
;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(利润=总收益-总成本)