对于在 上有意义的两个函数
上有意义的两个函数 与
与 ,如果对任意的
,如果对任意的 ,均有
,均有 ,则称
,则称 与
与 在
在 上是接近的,否则称
上是接近的,否则称 与
与 在
在 上是非接近的.现在有两个函数
上是非接近的.现在有两个函数 与
与 ,现给定区间
,现给定区间 .
.
(1)若 ,判断
,判断 与
与 是否在给定区间上接近;
是否在给定区间上接近;
(2)若 与
与 在给定区间
在给定区间 上都有意义,求
上都有意义,求 的取值范围;
的取值范围;
(3)讨论 与
与 在给定区间
在给定区间 上是否是接近的.
上是否是接近的.
将正三棱柱截去三个角(如图1所示A、B、C分别是
三边的中点)得到的几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为

| A. |
|
B. |
|
C. |
|
D. |
|
已知函数
(Ⅰ)当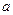 =1时,判断函数
=1时,判断函数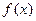 的单调性并写出其单调区间;
的单调性并写出其单调区间;
(Ⅱ)在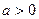 的条件下,若函数
的条件下,若函数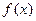 的图象与直线y=x至少有一个交点,求实数
的图象与直线y=x至少有一个交点,求实数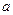 的取值范围。
的取值范围。
把边长为a的等边三角形铁皮如图(1)剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的底面为正三角形的直棱柱形容器(不计接缝)如图(2),设容器的高为x,容积为 。
。
(Ⅰ)写出函数 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(Ⅱ)求当x为多少时,容器的容积最大?并求出最大容积。
已知数列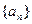 的前
的前 项和为
项和为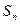 ,且满足
,且满足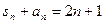 ,
,
(Ⅰ)求 ,
, ,
, 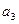 ,并猜想
,并猜想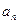 的表达式;
的表达式;
(Ⅱ)用数学归纳法证明所得的结论。
如图,已知抛物线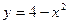 与直线
与直线 的两个交点分别为A、B,点P在抛物线上从A向B运动(点P不同于点A、B),
的两个交点分别为A、B,点P在抛物线上从A向B运动(点P不同于点A、B),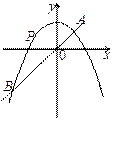
(Ⅰ)求由抛物线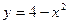 与直线
与直线 所围成的图形面积;
所围成的图形面积;
(Ⅱ)求使⊿PAB的面积为最大时P点的坐标。