求经过两条直线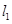 :
: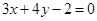 与
与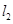 :
: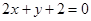 的交点
的交点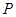 ,且垂直于直线
,且垂直于直线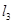 :
: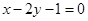 直线
直线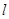 的方程.
的方程.
在平面直角坐标系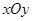 中,椭圆
中,椭圆 的中心为原点,焦点
的中心为原点,焦点 在
在 轴上,离心率为
轴上,离心率为 ,过点
,过点 的直线
的直线 交椭圆
交椭圆 于
于 两点,且
两点,且 的周长为16,求椭圆
的周长为16,求椭圆 的标准方程.
的标准方程.
已知双曲线 :
: 的离心率
的离心率 ,
, 、
、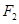 为其左右焦点,点
为其左右焦点,点 在
在 上,且
上,且 ,
, ,
, 是坐标原点.
是坐标原点.
(1)求双曲线 的方程;
的方程;
(2)过 的直线
的直线 与双曲线
与双曲线 交于
交于 两点,求
两点,求 的取值范围.
的取值范围.
袋中有6个球,其中4个白球,2个红球,从袋中任意取出两球,求下列事件的概率:
(1)A:取出的两球都是白球;
(2)B:取出的两球1个是白球,另1个是红球.
如图,在棱长为1的正方体 中,点
中,点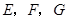 分别是
分别是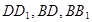 的中点.
的中点.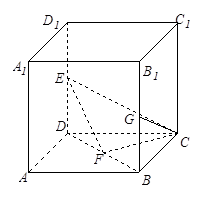
(1)求证: .
.
(2)求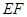 与
与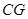 所成角的余弦值.
所成角的余弦值.
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
(1)求频率分布直方图中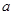 的值;
的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数.