为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)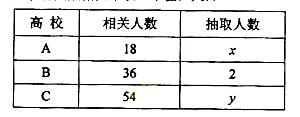
(Ⅰ)求x,y ;
(Ⅱ)若从高校B、C抽取的人中选2人作专题发言,求这二人都来自高校C的概率。
..(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分.
(理)如图,已知矩形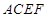 的边
的边 与正方形
与正方形 所在平面垂直,
所在平面垂直,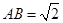 ,
,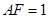 ,
,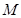 是线段
是线段 的中点。
的中点。
(1)求证: 平面
平面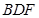 ;
;
(2)求二面角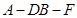 的大小。
的大小。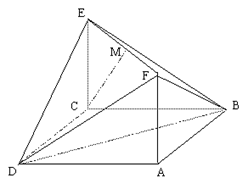
已知抛物线的顶点在坐标原点O,焦点F在x正半轴上,倾斜角为锐角的直线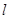 过F点。设直线
过F点。设直线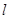 与抛物线交于A、B两点,与抛物线的准线交于M点,
与抛物线交于A、B两点,与抛物线的准线交于M点,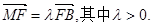
(I)若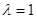 ,求直线
,求直线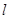 的斜率;
的斜率;
(II)若点A、B在x轴上的射影分别为A1、B1,且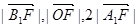 成等差数列,求
成等差数列,求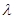 的值。
的值。
已知函数 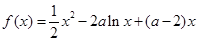 ,
,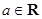 .
.
(Ⅰ)当  时,求函数
时,求函数  的最小值; (Ⅱ)当
的最小值; (Ⅱ)当 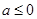 时,讨论函数
时,讨论函数  的单调性;
的单调性;
(Ⅲ)是否存在实数 ,对任意的
,对任意的  ,且
,且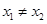 ,有
,有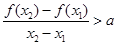 ,恒成立,若存在求出
,恒成立,若存在求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
如图,在四棱锥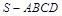 中,平面
中,平面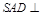 平面
平面 .底面
.底面 为矩形,
为矩形, 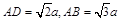 ,
,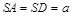 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角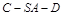 的大小.
的大小.
数列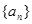 的前
的前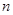 项和记为
项和记为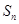 ,
, ,点
,点 在直线
在直线 上,
上, .
.
(Ⅰ)当实数 为何值时,数列
为何值时,数列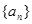 是等比数列?
是等比数列?
(Ⅱ)在(Ⅰ)的结论下,设 ,
,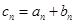 ,
, 是数列
是数列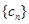 的前
的前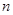 项和,求
项和,求 。
。