(本小题满分12分)
某工厂现有80台机器,每台机器平均每天生产384件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,由于其他生产条件没变,因此每增加一台机器,每台机器平均每天将少生产4件产品.
(Ⅰ)如果增加x台机器,每天的生产总量为 件,请你写出
件,请你写出 与
与 之间的关系式;
之间的关系式;
(Ⅱ)增加多少台机器,可以使每天的生产总量最大?最大生产总量是多少?
解不等式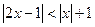
已知 是椭圆
是椭圆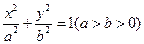 的左、右焦点,过点
的左、右焦点,过点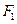 作
作
倾斜角为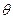 的动直线
的动直线 交椭圆于
交椭圆于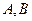 两点.当
两点.当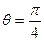 时,
时, ,且
,且 .
.
(1)求椭圆的离心率及椭圆的标准方程;
(2)求△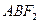 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线 的方程.
的方程.
已知函数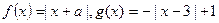 .
.
(1)解关于 的不等式
的不等式 ;
;
(2)若对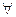
 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知直线 的参数方程为
的参数方程为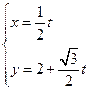 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是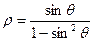 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点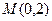 ,直线
,直线 与曲线C交于A,B两点.
与曲线C交于A,B两点.
(1)写出直线 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA|·|MB|的值.
某校高三某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都
受到不同程度的破坏,但可见部分如下,据此解答如下问题: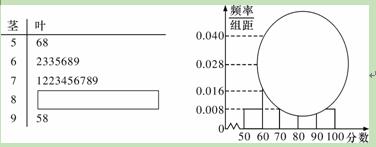
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求分数在[90,100]之间的份数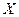 的数学期望
的数学期望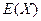 .
.