已知 是椭圆
是椭圆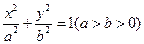 的左、右焦点,过点
的左、右焦点,过点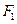 作
作
倾斜角为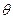 的动直线
的动直线 交椭圆于
交椭圆于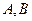 两点.当
两点.当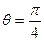 时,
时, ,且
,且 .
.
(1)求椭圆的离心率及椭圆的标准方程;
(2)求△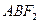 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线 的方程.
的方程.
集合 是由适合以下性质的函数组成:对于任意
是由适合以下性质的函数组成:对于任意 ,
, ,且
,且 在
在 上是增函数,
上是增函数,
(1)试判断 及
及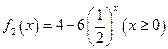 是否在集合
是否在集合 中,若不在
中,若不在 中,试说明理由;
中,试说明理由;
(2)对于(1)中你认为集合 中的函数
中的函数 ,不等式
,不等式
 是否对任意
是否对任意
 恒成立,试证明你的结论.
恒成立,试证明你的结论.
已知函数 且
且 ,
,
(1)求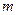 的值;
的值;
(2)判定 的奇偶性;
的奇偶性;
(3)判断 在
在 上的单调性,并给予证明.
上的单调性,并给予证明.
已知函数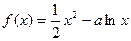

(1)若函数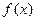 在
在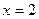 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值;
(2)若函数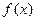 在
在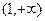 为增函数,求
为增函数,求 的取值范围;
的取值范围;
(3)讨论方程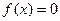 解的个数,并说明理由。
解的个数,并说明理由。
已知菱形
的顶点
在椭圆
上,对角线
所在直线的斜率为
.
(Ⅰ)当直线
过点
时,求直线
的方程;
(Ⅱ)当
时,求菱形
面积的最大值.
已知函数 (其中
(其中 为自然对数的底).
为自然对数的底).
(1)求函数 的最小值;
的最小值;
(2)若 ,证明:
,证明: