已知菱形
的顶点
在椭圆
上,对角线
所在直线的斜率为
.
(Ⅰ)当直线
过点
时,求直线
的方程;
(Ⅱ)当
时,求菱形
面积的最大值.
已知命题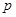 :方程
:方程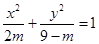 表示焦点在
表示焦点在 轴上的椭圆;命题
轴上的椭圆;命题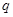 :双曲线
:双曲线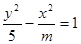 的离心率
的离心率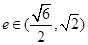 .若
.若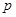 或
或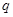 为真命题,
为真命题,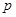 且
且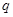 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
解关于 的不等式:
的不等式: (
(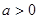 )
)
对于定义在实数集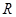 上的两个函数
上的两个函数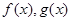 ,若存在一次函数
,若存在一次函数 使得,对任意的
使得,对任意的 ,都有
,都有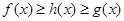 ,则把函数
,则把函数 的图像叫函数
的图像叫函数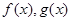 的“分界线”。现已知
的“分界线”。现已知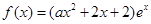 (
( ,
,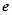 为自然对数的底数),
为自然对数的底数),
(1)求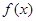 的递增区间;
的递增区间;
(2)当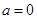 时,函数
时,函数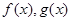 是否存在过点
是否存在过点 的“分界线”?若存在,求出函数
的“分界线”?若存在,求出函数 的解析式,若不存在,请说明理由。
的解析式,若不存在,请说明理由。
已知椭圆 :
: (
(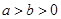 )过点
)过点 ,其左、右焦点分别为
,其左、右焦点分别为 ,且
,且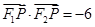 .
.
(1)求椭圆 的方程;
的方程;
(2)若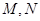 是直线
是直线 上的两个动点,且
上的两个动点,且 ,则以
,则以 为直径的圆
为直径的圆 是否过定点?请说明理由.
是否过定点?请说明理由.
已知数列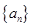 满足:
满足: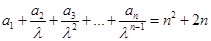 (其中常数
(其中常数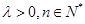 ).
).
(1)求数列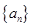 的通项公式;
的通项公式;
(2)当 时,数列
时,数列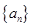 中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。
中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。