.(本小题满分12分)
如图,四棱锥P—ABCD中,底面ABCD是边长为 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=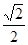 AD.
AD.
(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
已知O为坐标原点, ,
,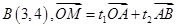 .
.
(1)求点M在第二象限或第三象限的充要条件;
(2)求证:当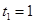 时,不论
时,不论 为何实数,A、B、M三点都共线;
为何实数,A、B、M三点都共线;
(3)若  ,求当点M为
,求当点M为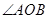 的平分线上点时
的平分线上点时 的值.
的值.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为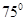 ,
,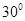 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为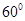 ,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,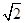
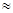 1. 414,
1. 414, 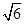
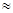 2.449)
2.449)
右图为函数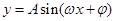 的一段图象.
的一段图象.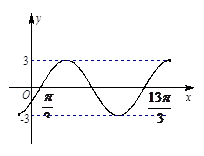
(1)请写出这个函数的一个解析式;
(2)求与(1)中函数图象关于直线 对称的函数图象的解析式,并作出它一个周期内的简图.
对称的函数图象的解析式,并作出它一个周期内的简图.
若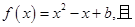
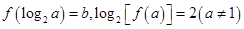 .
.
(1)求 的最小值及对应的
的最小值及对应的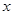 值;
值;
(2)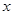 取何值时,
取何值时, 且
且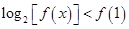
已知向量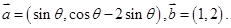
(1)若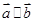 ,求
,求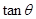 的值;
的值;
(2)若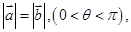 求
求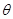 的值;
的值;
(3)设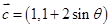 ,若
,若 求
求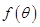 的值域.
的值域.