函数 是R上的偶函数,且当
是R上的偶函数,且当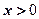 时,函数的解析式为
时,函数的解析式为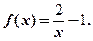
(1)求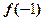 的值;
的值;
(2)用定义证明 在
在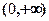 上是减
上是减 函数;
函数;
(3)求当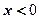 时,函数的解析式;[来源
时,函数的解析式;[来源
已知函数f(x)=2 sinxcosx-2cos2x+l.
sinxcosx-2cos2x+l.
(I)求f(x)的最小正周期;
(Ⅱ)若 ∈(0,
∈(0, ),且f(
),且f( )=1,求
)=1,求 的值。
的值。
若无穷数列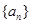 满足:①对任意
满足:①对任意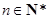 ,
,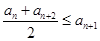 ;②存在常数
;②存在常数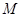 ,对任意
,对任意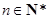 ,
,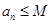 ,则称数列
,则称数列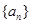 为“
为“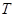 数列”.
数列”.
(Ⅰ)若数列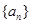 的通项为
的通项为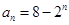
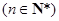 ,证明:数列
,证明:数列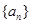 为“
为“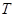 数列”;
数列”;
(Ⅱ)若数列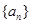 的各项均为正整数,且数列
的各项均为正整数,且数列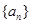 为“
为“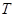 数列”,证明:对任意
数列”,证明:对任意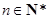 ,
,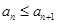 ;
;
(Ⅲ)若数列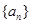 的各项均为正整数,且数列
的各项均为正整数,且数列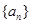 为“
为“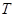 数列”,证明:存在
数列”,证明:存在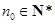 ,数列
,数列 为等差数列.
为等差数列.
已知椭圆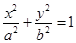
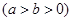 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为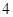 ,且过点
,且过点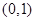 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)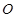 为坐标原点,斜率为
为坐标原点,斜率为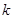 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点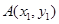 ,
,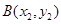 ,若
,若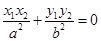 ,求△
,求△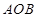 的面积.
的面积.
已知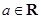 ,函数
,函数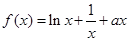 .
.
(Ⅰ)当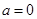 时,求
时,求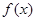 的最小值;
的最小值;
(Ⅱ)若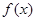 在区间
在区间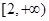 上是单调函数,求
上是单调函数,求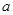 的取值范围.
的取值范围.
如图,在三棱柱 中,
中, 平面
平面 ,
, ,
,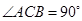 ,
, 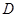 ,
,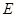 分别是
分别是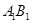 ,
, 的中点.
的中点.
(Ⅰ)求证: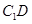 ∥平面
∥平面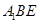 ;
;
(Ⅱ)求证:平面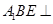 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面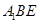 所成角的正弦值.
所成角的正弦值.