(本小题满分12分)
已知椭圆 的离心率
的离心率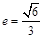 ,过点
,过点 和
和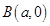 的直线与原点的距离为
的直线与原点的距离为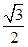 。⑴求椭圆的方程;⑵已知定点
。⑴求椭圆的方程;⑵已知定点 ,若直线
,若直线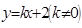 与椭圆交于
与椭圆交于 两点,问:是否存在
两点,问:是否存在 的值,使以
的值,使以 为直径的圆过
为直径的圆过 点?请说明理由。
点?请说明理由。
2012年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类: 第一类的用电区间在 ,第二类在
,第二类在 ,第三类在
,第三类在 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
⑴ 求该小区居民用电量的中位数与平均数;
⑵ 本月份该小区没有第三类的用电户出现,为鼓励居民节约用电,供电部门决定:对第一类每户奖励20元钱,第二类每户奖励5元钱,求每户居民获得奖励的平均值;
⑶ 利用分层抽样的方法从该小区内选出5户居民代表,若从该5户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率. 
在三角形 中,
中,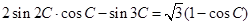 .
.
⑴ 求角 的大小;
的大小;
⑵ 若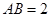 ,且
,且 ,求
,求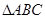 的面积.
的面积.
设函数 ,
,
 .
.
⑴ 求不等式 的解集;
的解集;
⑵ 如果关于 的不等式
的不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 ,
,
以原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
⑴ 求曲线 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;
⑵ 当 时,曲线
时,曲线 和
和 相交于
相交于 、
、 两点,求以线段
两点,求以线段 为直径的圆的直角坐标方程.
为直径的圆的直角坐标方程.
如图, 是
是 的直径,弦
的直径,弦 与
与 垂直,并与
垂直,并与 相交于点
相交于点 ,点
,点 为弦
为弦 上异于点
上异于点 的任意一点,连结
的任意一点,连结 、
、 并延长交
并延长交 于点
于点 、
、 .
.
⑴ 求证: 、
、 、
、 、
、 四点共圆;
四点共圆;
⑵ 求证: .
.