在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF. 连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t. 
⑴ 求tan∠FOB的
 值;
值;⑵用含t的代数式表示△OAB的面积S;
⑶是否存在点C,使以B,E,F为顶点的三角形与△OFE相似,若存在,请求出所有满足要求的B点的坐标;若不存在,请说明理由.
某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为 为正整数).
根据题意,填写下表:
|
游泳次数 |
10 |
15 |
20 |
|
|
|
方式一的总费用(元 |
150 |
175 |
|
|
|
|
方式二的总费用(元 |
90 |
135 |
|
|
|
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当 时,小明选择哪种付费方式更合算?并说明理由.
如图,甲、乙两座建筑物的水平距离 为 ,从甲的顶部 处测得乙的顶部 处的俯角为 ,测得底部 处的俯角为 ,求甲、乙建筑物的高度 和 (结果取整数).参考数据: , .

已知 是 的直径,弦 与 相交, ,
如图①,若 为 的中点,求 和 的大小;
(Ⅱ)如图②,过点 作 的切线,与 的延长线交于点 ,若 ,求 的大小.

某养鸡场有2500只鸡准备对外出售,从中随机抽取了一部分鸡,根据它们的质量(单位: ,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
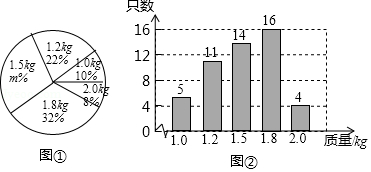
图①中 的值为 ;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计这2500只鸡中,质量为 的约有多少只?
解不等式组
请结合题意填空,完成本题的解答.
解不等式①,得 ;
解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为 .
