如图，二次函数y＝ax2－2ax＋的图象与x轴交于A、B二点，与y轴交于C点．抛物线的顶点为E（1，2），D为抛物线上一点，且CD∥x轴．
（1）求此二次函数的关系式；
（2）写出A、B、C、D四点的坐标；
（3）若点F在抛物线的对称轴
上，点G在抛物线上，且以A、B、F、G四点为顶点的四边形为平行四边形，求点G 的坐标．
已知关于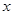
的一元二次方程x2+2x+3k-6=0有两个不相等的实数根
（1）求实数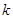
的取值范围；
（2）若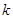为正整数，且该方程的根都是整数，求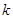的值．
列方程或方程组解应用题：
一列“和谐号”动车组，有一等车厢和二等车厢共6节，一共设有座位496个．其中每节一等车厢设有座位64个，每节二等车厢设有座位92个．问该列车一等车厢和二等车厢各有多少节？
解分式方程：
已知：如图，C是AE上一点，∠B=∠DAE，BC∥DE，AC=DE．求证：AB=DA．
在平面直角坐标系中，已知抛物线
(b，c为常数)的顶点为P，等腰直角三角形ABC的顶点A的坐标为(0，–1)，C的坐标为(4，3)，直角顶点B在第四象限．
(1)如图，若该抛物线过A，B两点，求b，c的值；
(2)平移(1)中的抛物线，使顶点P在直线AC上滑动，且与直线AC交于另一点Q．
①点M在直线AC下方，且为平移前(1)中的抛物线上的点，当以M，P，Q三点为顶点的三角形是以PQ为腰的等腰直角三角形时，求点M的坐标；
②取BC的中点N，连接NP，BQ．当
取最大值时，点Q的坐标为________.