某中学标准化建设规划在校园内的一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草(如图所示),若使每一块草坪的面积都为96平方米.设人行道的宽为x米,下列方程: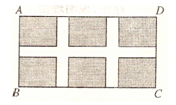
①(36-2x)(20-x)=96×6;
②2×20x+(36-2x)x=36×20-96×6;
③ (18-x)(10-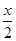 )=
)= ×96×6,其中正确的个数为( )
×96×6,其中正确的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
sin30°的值是 ()
| A.1 | B.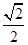 |
C.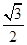 |
D.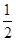 |
如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形依次进行下去,则第n个内接正方形的边长为()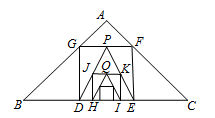
A.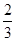 ·(
·(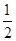 )n B.
)n B.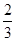
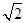 ·(
·(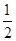 )n
)n
C.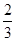 ·(
·(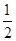 )n-1D.
)n-1D.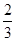
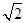 ·(
·(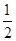 )n-
)n-
如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为()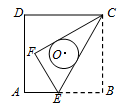
A.4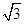 |
B.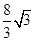 |
C.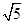 |
D.2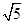 |
下列说法中,不正确的是()
| A.过圆心的弦是圆的直径 |
| B.等弧的长度一定相等 |
| C.周长相等的两个圆是等圆 |
| D.同一条弦所对的两条弧一定是等弧 |
如图,⊙O的半径OA=10cm,弦AB=16cm,P为AB上一动点,则点P到圆心O的最短距离为()
| A.4cm | B.5cm | C.6cm | D.7cm |