如图:已知三棱锥 中,
中, 面
面 ,
, ,
, ,
, 为
为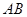 上一点,
上一点,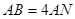 ,
, 分别为
分别为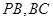 的中点.
的中点.
(1)证明: .
.
(2)求面 与面
与面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(3)在线段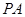 (包括端点)上是否存在一点
(包括端点)上是否存在一点 ,使
,使 平面
平面 ?若存在,确定
?若存在,确定 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.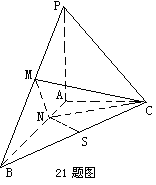
集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},
C={x|x2+2x-8=0}.
(1)若A∩B=A∪B,求a的值;
(2)若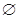
 A∩B,A∩C=
A∩B,A∩C=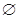 ,求a的值
,求a的值
设函数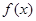 是定义在
是定义在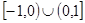 上的奇函数,当
上的奇函数,当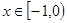 时,
时,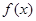
 为实数);
为实数);
(1)当 时,求函数
时,求函数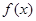 的解析式;
的解析式;
(2)若 ,试判断
,试判断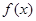 在
在 上的单调性;
上的单调性;
(3)是否存在a,使得当 时,
时,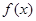 有最大值
有最大值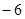 。
。
在调查男女乘客是否晕机的情况中,已知男乘客占总调查人数的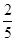 ,其中有一半会晕机,而女乘客只有
,其中有一半会晕机,而女乘客只有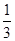 的人会晕机,经过调查员的计算:有95%以上的把握认为是否晕机与性别有关,那么被调查的人中最少有多少人会晕机? 参考: P(k
的人会晕机,经过调查员的计算:有95%以上的把握认为是否晕机与性别有关,那么被调查的人中最少有多少人会晕机? 参考: P(k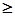 3.841)=0.05
3.841)=0.05
解不等式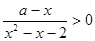
数列{an}(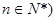 中,a1=1,点(an,an+1)在直线
中,a1=1,点(an,an+1)在直线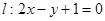 上;
上;
(1)设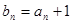 ,求证数列{bn}是等比数列;
,求证数列{bn}是等比数列;
(2)设 ,求{cn}的通项公式;
,求{cn}的通项公式;