设函数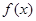 是定义在
是定义在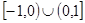 上的奇函数,当
上的奇函数,当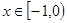 时,
时,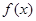
 为实数);
为实数);
(1)当 时,求函数
时,求函数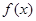 的解析式;
的解析式;
(2)若 ,试判断
,试判断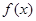 在
在 上的单调性;
上的单调性;
(3)是否存在a,使得当 时,
时,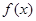 有最大值
有最大值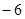 。
。
(本题满分13分)
已知数列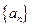 对
对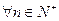 都有
都有
(Ⅰ)求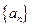 的通项
的通项 ;
;
(Ⅱ)设数列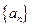
 的前n项和为
的前n项和为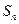 , 求证:对
, 求证:对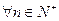 ,
, 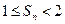 .
.
(本题满分12分)
已知⊙O: ,直线
,直线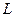 交⊙O于A、B两点,分别过A、B作⊙O的切线,交于M点。
交⊙O于A、B两点,分别过A、B作⊙O的切线,交于M点。
(Ⅰ) 当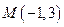 时,求弦长AB;
时,求弦长AB;
(Ⅱ) 若直线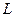 过点(1,1),求点
过点(1,1),求点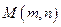 的轨迹
的轨迹 方程。
方程。
(本题满分12分)
已知函数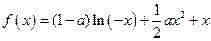
(I)如果 在
在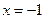 处的切线过(0,1)点,求
处的切线过(0,1)点,求 的值;
的值;
(II)若函数 在
在 为增函数,求实数
为增函数,求实数 的取值范围。
的取值范围。
(本题满分12分)
已知函数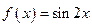 ,
,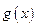 与
与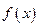 图象关于点
图象关于点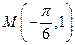 对称,
对称,
记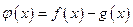
(Ⅰ) 求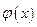 的最小正周期,单调增区间;
的最小正周期,单调增区间;
(Ⅱ) 若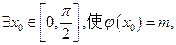 求
求 的最小值。
的最小值。
(本题满分12分)
在△ABC中,∠A、∠B、∠C所对的边长为a、b、c,已知
(Ⅰ)求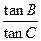 的值;
的值;
(Ⅱ)求∠A的取值范围。